```{r, include = FALSE}
current_file <- knitr::current_input()
basename <- gsub(".Rmd$", "", current_file)
```
```{r, include = FALSE, eval = F}
input <- fs::path_ext_set(current_file, "html")
pagedown::chrome_print(input = input, format = "pdf", wait = 20)
```
```{r, include = FALSE}
knitr::opts_chunk$set(
fig.path = sprintf("images/%s/", basename),
fig.width = 6,
fig.height = 4,
fig.align = "center",
out.width = "100%",
fig.retina = 3,
echo = FALSE,
warning = FALSE,
message = FALSE,
cache = FALSE
)
```
```{r}
library(tidyverse)
library(fabricerin)
```
```{r titleslide, child="assets/titleslide.Rmd"}
```
---
class: transition middle animated slideInLeft
## Easy summaries -- numerical and graphical
---
# Hinges and 5-number summaries
.pull-left[
.font_smaller[
```{r}
options(width=25)
x <- c(-3.2, -1.7, -0.4, 0.1, 0.3, 1.2, 1.5, 1.8, 2.4, 3.0, 4.3, 6.4, 9.8)
x
```
]
You know the median is the middle number. What's a hinge?
There are 13 data values here, provided already sorted. We are going to write them into a Tukey named down-up-down-up pattern, evenly.
.font_smaller[.monash-blue2[Median will be 7th, hinge will be 4th from each end.]]
]
.pull-right[
```{r}
fabric_drawing(cid = "canvas3",
cwidth = 550,
cheight = 500,
cfill = "whitesmoke",
drawingWidth = 3,
gumSize = 10)
```
]
---
# Hinges and 5-number summary
.pull-left[
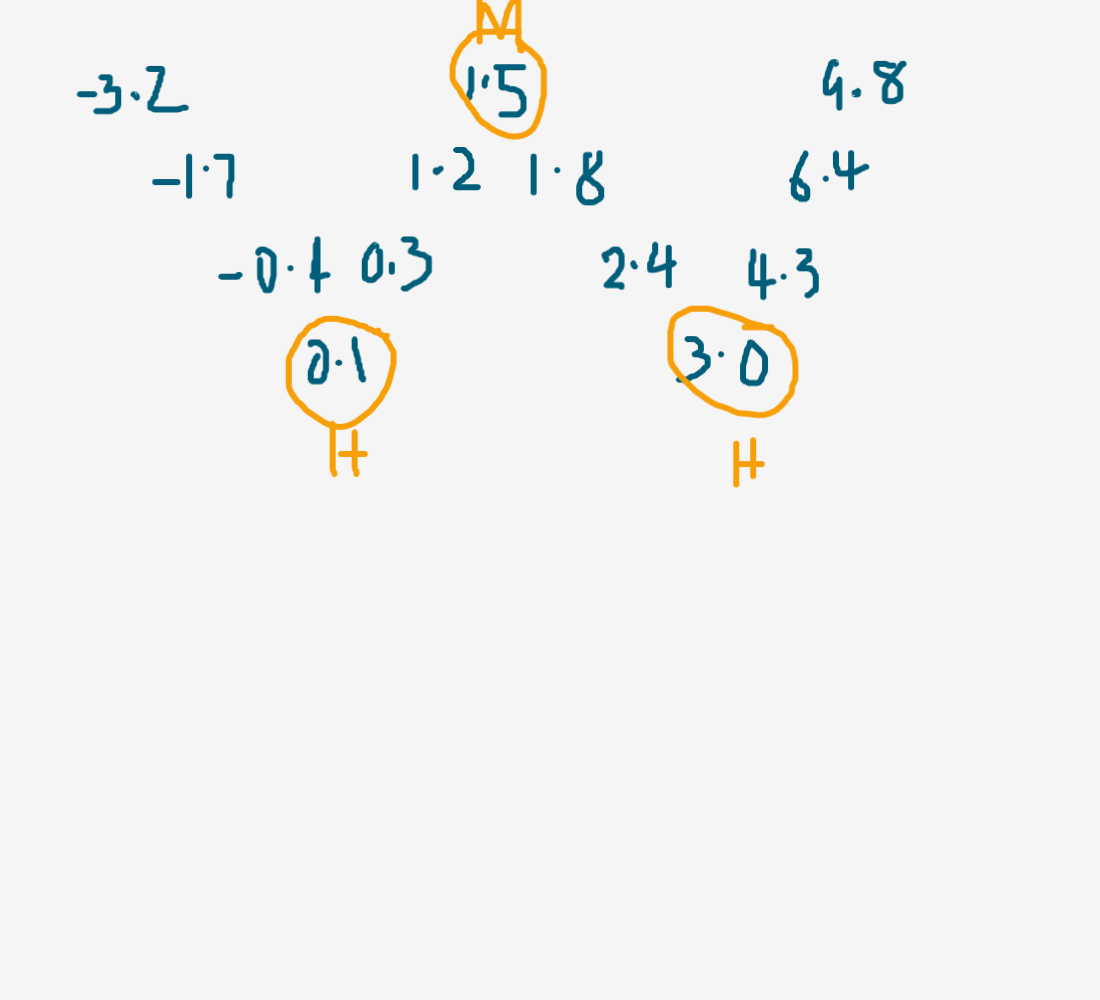 ]
.pull-right[
]
.pull-right[
 ]
hinges are alternatively known as Q1 and Q3.
---
# box-and-whisker display
.pull-left[
]
hinges are alternatively known as Q1 and Q3.
---
# box-and-whisker display
.pull-left[
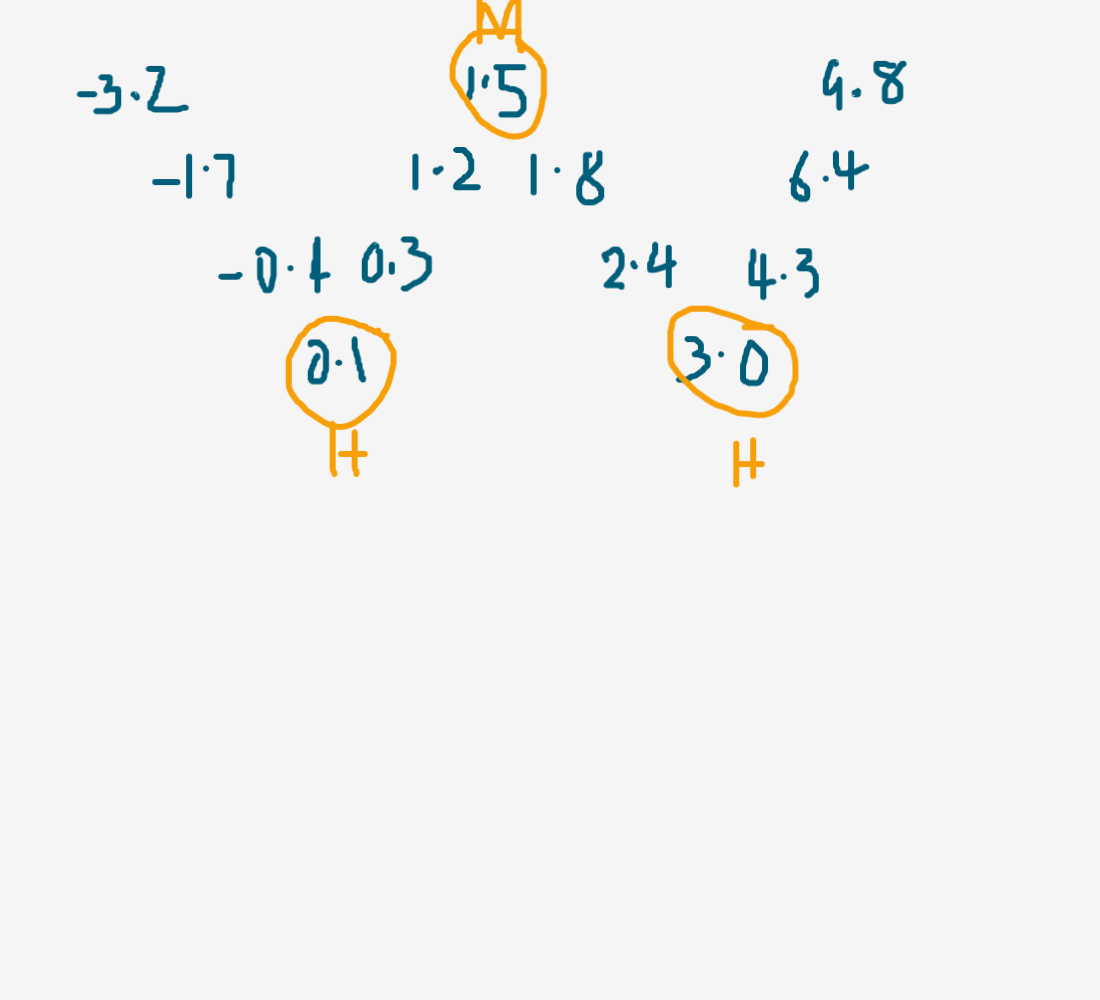 ]
.pull-right[
Starting with a 5-number summary
]
.pull-right[
Starting with a 5-number summary
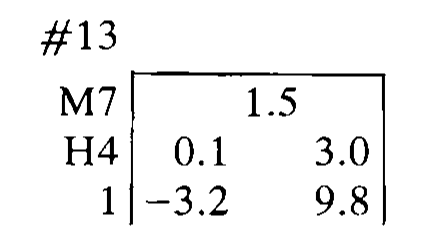 ]
---
# box-and-whisker display
.pull-left[
Starting with a 5-number summary
]
---
# box-and-whisker display
.pull-left[
Starting with a 5-number summary
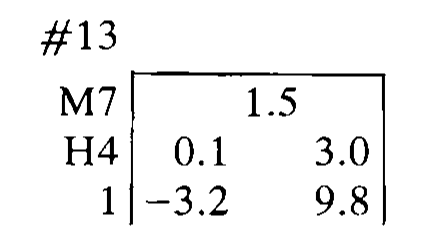 ]
.pull-right[
```{r}
fabric_drawing(cid = "canvas4",
cwidth = 550,
cheight = 500,
cfill = "whitesmoke",
drawingWidth = 3,
gumSize = 10)
```
]
---
# Identified end values
.pull-left[
]
.pull-right[
```{r}
fabric_drawing(cid = "canvas4",
cwidth = 550,
cheight = 500,
cfill = "whitesmoke",
drawingWidth = 3,
gumSize = 10)
```
]
---
# Identified end values
.pull-left[
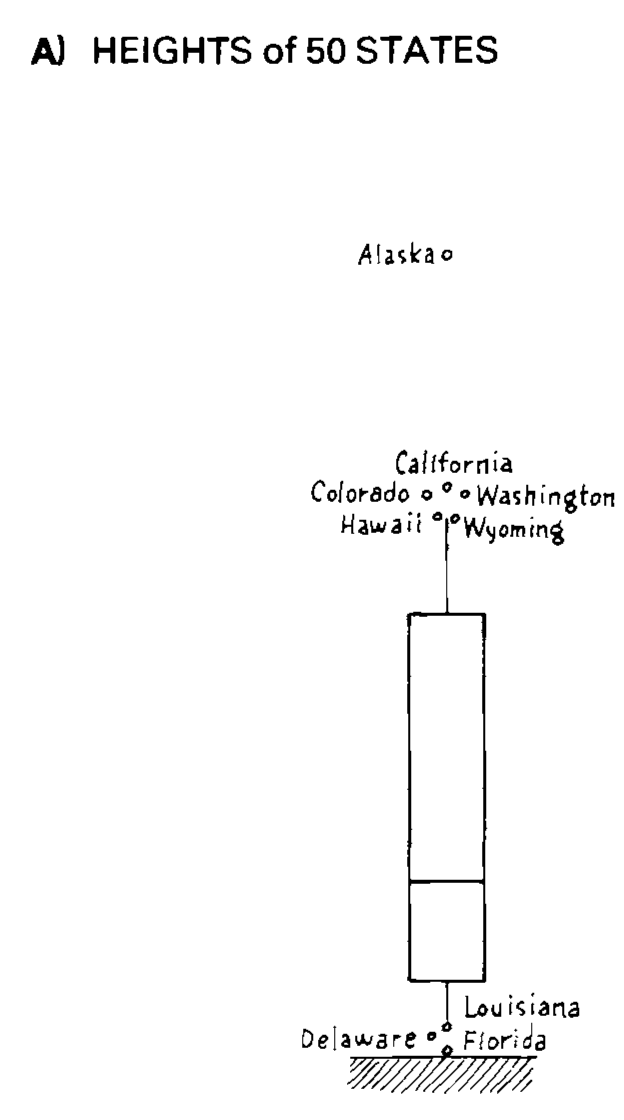 Why are some individual points singled out?
]
.pull-right[
Why are some individual points singled out?
]
.pull-right[
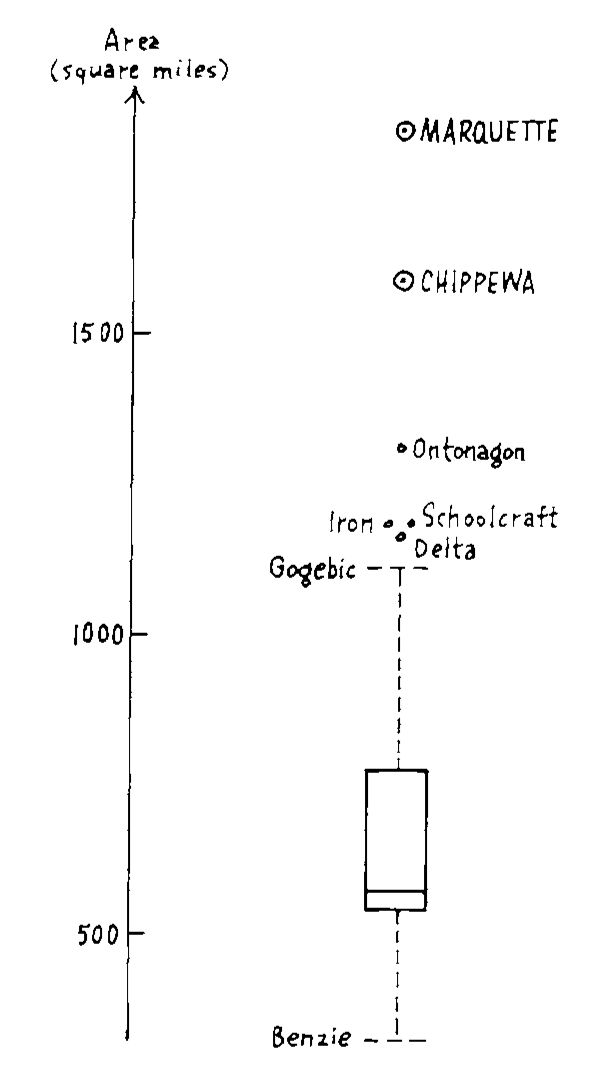 Rules for this one may be clearer?
]
---
class: motivator middle center
## `r emo::ji("scream_cat")` Isn't this imposing a belief?
---
class: middle center
.outline-text[## There is no excuse for failing to plot and look]
Rules for this one may be clearer?
]
---
class: motivator middle center
## `r emo::ji("scream_cat")` Isn't this imposing a belief?
---
class: middle center
.outline-text[## There is no excuse for failing to plot and look]
.font_smaller[Another Tukey wisdom drop]
---
background-image: \url(images/lecture-02B/schematic.png)
background-size: 20%
background-position: 99% 50%
# Fences and outside values
- H-spread: difference between the hinges (we would call this Inter-Quartile Range)
- step: 1.5 times H-spread
- inner fences: 1 step outside the hinges
- outer fences: 2 steps outside the hinges
- the value at each end closest to, but still inside the inner fence are "adjacent"
- values between an inner fence and its neighbouring outer fence are "outside"
- values beyond outer fences are "far out"
- these rules produce a SCHEMATIC PLOT
---
# New statistics: trimeans
The number that comes closest to
$$\frac{\text{lower hinge} + 2\times \text{median} + \text{upper hinge}}{4}$$
is the **trimean**.
Think about trimmed means, where we might drop the highest and lowest 5% of observations.
---
# Letter value plots
.pull-left[
Why break the data into quarters? Why not eighths, sixteenths? k-number summaries?
What does a 7-number summary look like?
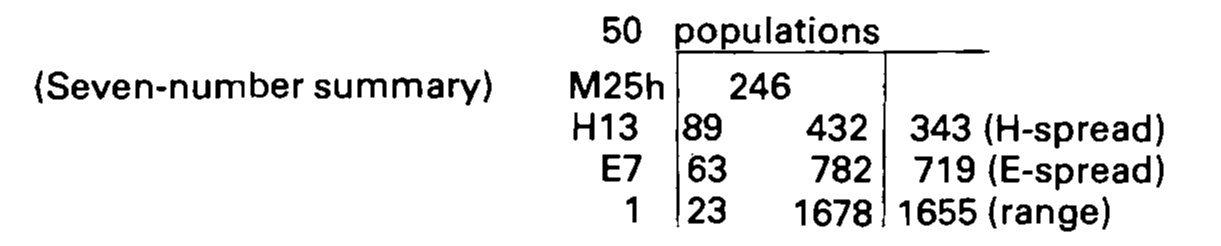 .monash-orange2[How would you make an 11-number summary?]
]
.pull-right[
.font_smaller[
```{r lvplot, echo=TRUE}
library(lvplot)
p <- ggplot(mpg,
aes(class, hwy))
p + geom_lv(aes(fill=..LV..)) + #<<
scale_fill_brewer()
```
]
]
---
class: informative middle
## Box plots are ubiquitous in use today.
`r emo::ji("dog")` `r emo::ji("cat")` Mostly used to compare distributions, multiple subsets of the data.
Puts the emphasis on the `r anicon::nia("middle 50%", animate="spin", anitype="hover", color="yellow")` of observations, although variations can put emphasis on other aspects.
---
class: transition middle animated slideInLeft
## Easy re-expression
---
# Logs, square roots, reciprocals
.pull-left[
What you need to know about logs?
- how to find good enough logs fast and easily
- that equal differences in logs correspond to equal ratios of raw values. .font_smaller[(This means that wherever you find people using products or ratios-- even in such things as price indexes--using logs--thus converting producers to sums and ratios to differences--is likely to help.)]
]
--
.pull-right[
The most common transformations are logs, sqrt root, reciprocals, reciprocals of square roots
-1, -1/2, +1/2, +1
What happened to ZERO?
--
`r anicon::nia("It turns out that the role of a zero power, is for the purposes of re-expression, neatly filles by the logarithm.", animate="passing", anitype="hover", size=0.5)`
]
---
## Re-express to symmetrize the distribution
.monash-orange2[How would you make an 11-number summary?]
]
.pull-right[
.font_smaller[
```{r lvplot, echo=TRUE}
library(lvplot)
p <- ggplot(mpg,
aes(class, hwy))
p + geom_lv(aes(fill=..LV..)) + #<<
scale_fill_brewer()
```
]
]
---
class: informative middle
## Box plots are ubiquitous in use today.
`r emo::ji("dog")` `r emo::ji("cat")` Mostly used to compare distributions, multiple subsets of the data.
Puts the emphasis on the `r anicon::nia("middle 50%", animate="spin", anitype="hover", color="yellow")` of observations, although variations can put emphasis on other aspects.
---
class: transition middle animated slideInLeft
## Easy re-expression
---
# Logs, square roots, reciprocals
.pull-left[
What you need to know about logs?
- how to find good enough logs fast and easily
- that equal differences in logs correspond to equal ratios of raw values. .font_smaller[(This means that wherever you find people using products or ratios-- even in such things as price indexes--using logs--thus converting producers to sums and ratios to differences--is likely to help.)]
]
--
.pull-right[
The most common transformations are logs, sqrt root, reciprocals, reciprocals of square roots
-1, -1/2, +1/2, +1
What happened to ZERO?
--
`r anicon::nia("It turns out that the role of a zero power, is for the purposes of re-expression, neatly filles by the logarithm.", animate="passing", anitype="hover", size=0.5)`
]
---
## Re-express to symmetrize the distribution
 ---
class: center middle
## Power ladder
---
class: center middle
## Power ladder
`r anicon::faa("arrow-left", animate="passing", color="orangered", anitype="hover")` `r anicon::nia("fix RIGHT-skewed values", animate="passing", color="orangered", anitype="hover")`
-2, -1, -1/2, 0 (log), 1/3, 1/2, .font_large[.monash-orange2[1]], 2, 3, 4
`r anicon::faa("arrow-right", animate="passing-reverse", color="orangered", anitype="hover")` `r anicon::nia("fix LEFT-skewed values", animate="passing-reverse", color="orangered", anitype="hover")`
---
class: middle center
.outline-text[## We now regard re-expression as a tool, something to let us do a better job of grasping. The grasping is done with the eye and the better job is through a more symmetric appearance.]
.font_smaller[Another Tukey wisdom drop]
---
# Linearising bivariate relationships
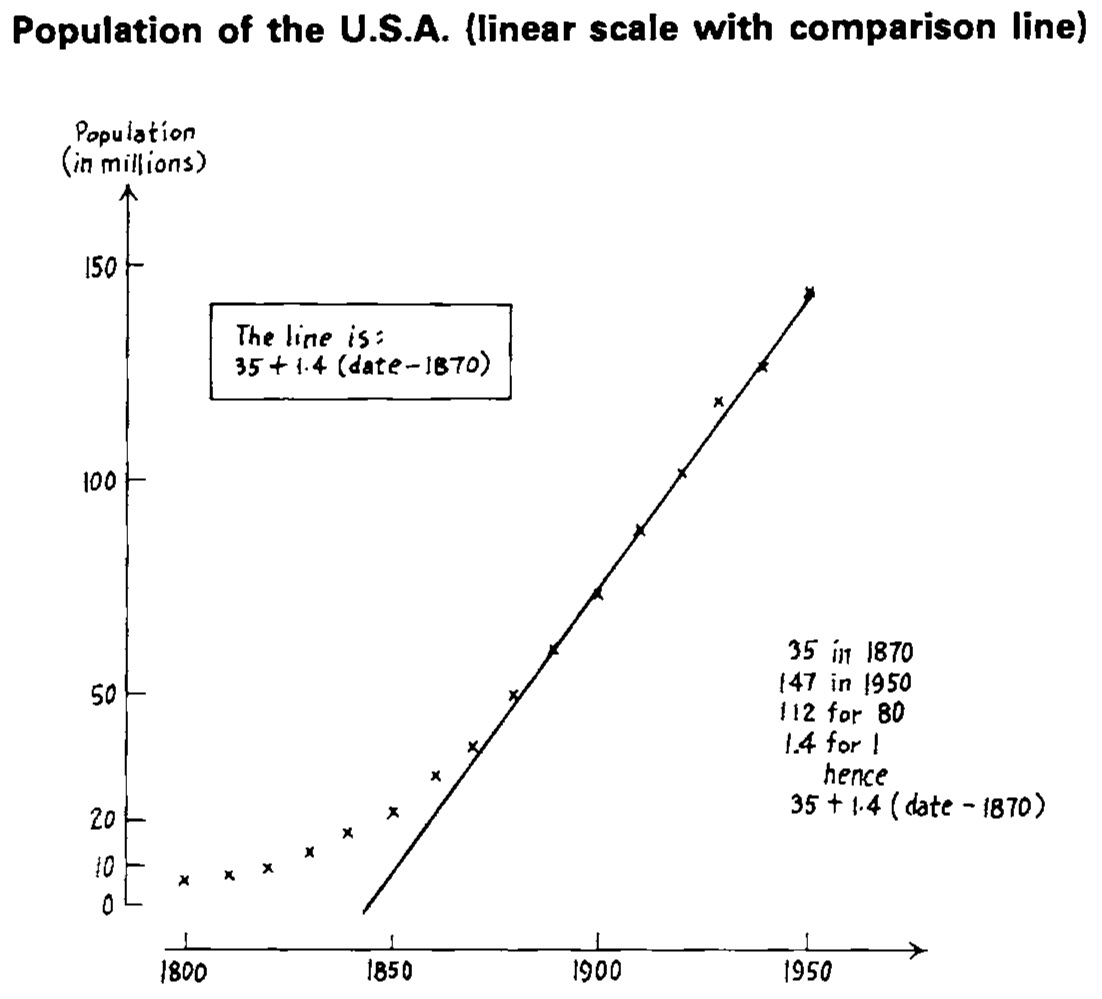
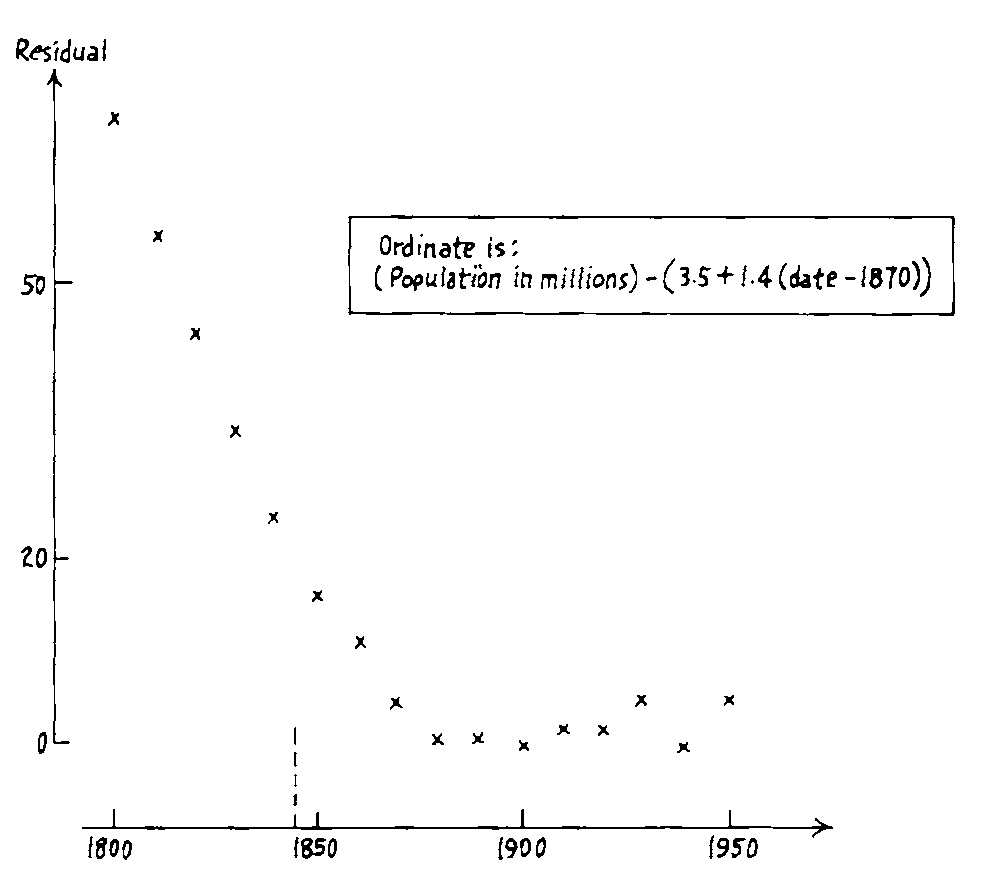
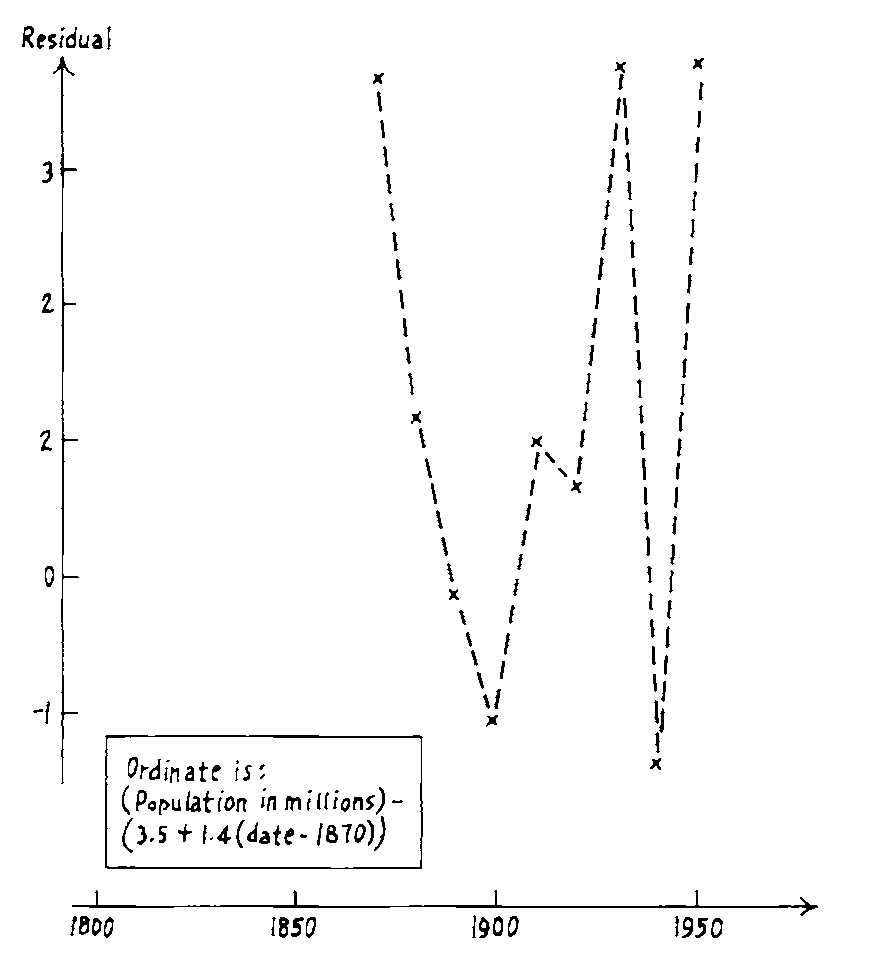
.monash-orange2[Surprising observation: The small fluctuations in later years]. Apparently these were tracked down to be data collection errors or problems. .monash-blue2[I think there is another possible reason. Do you?]
---
# Linearising bivariate relationships
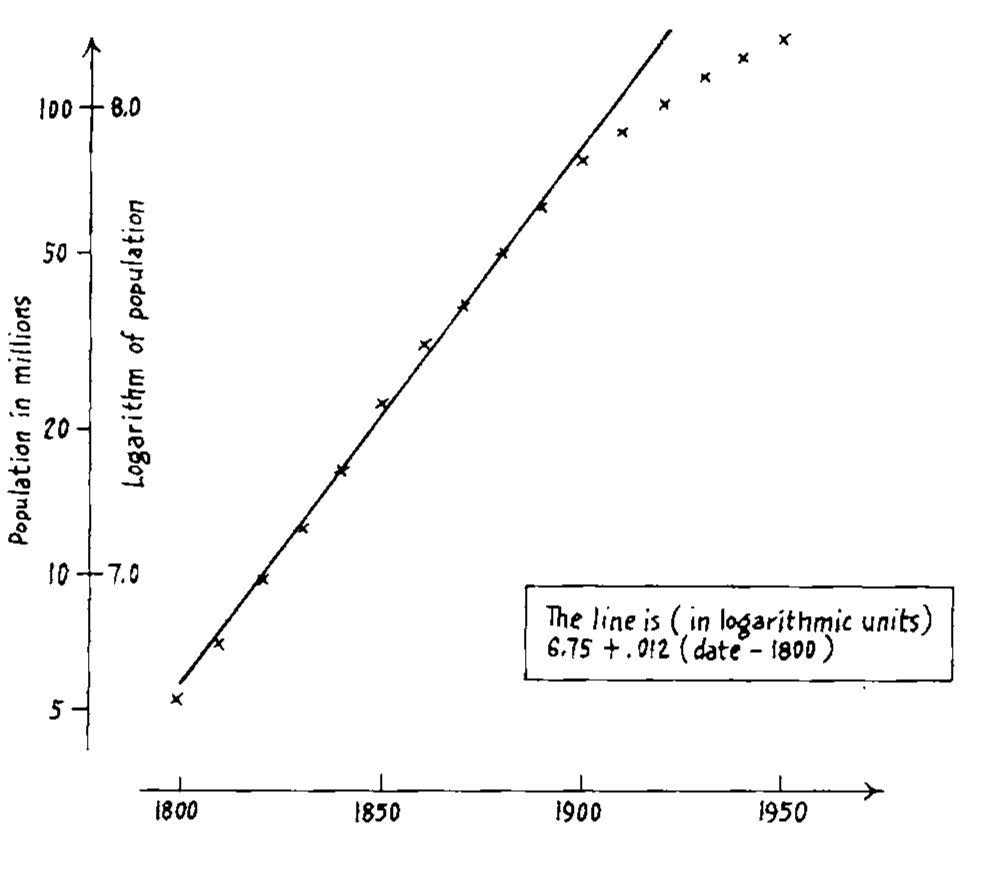
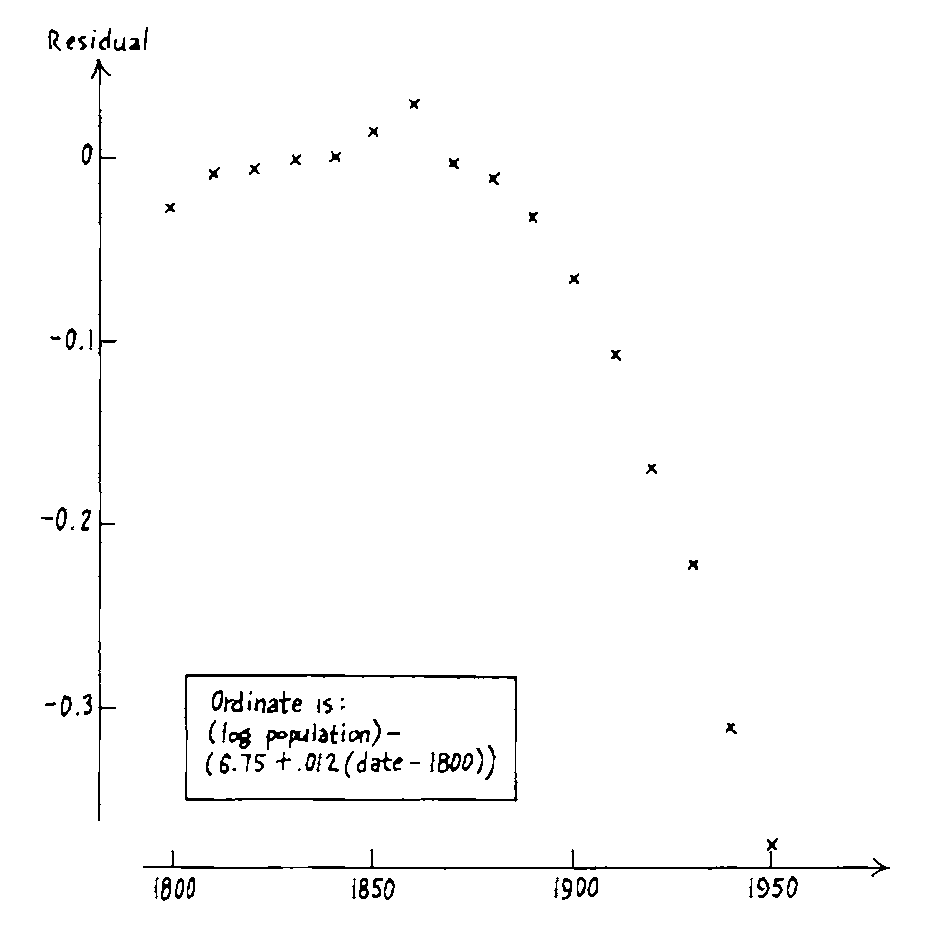
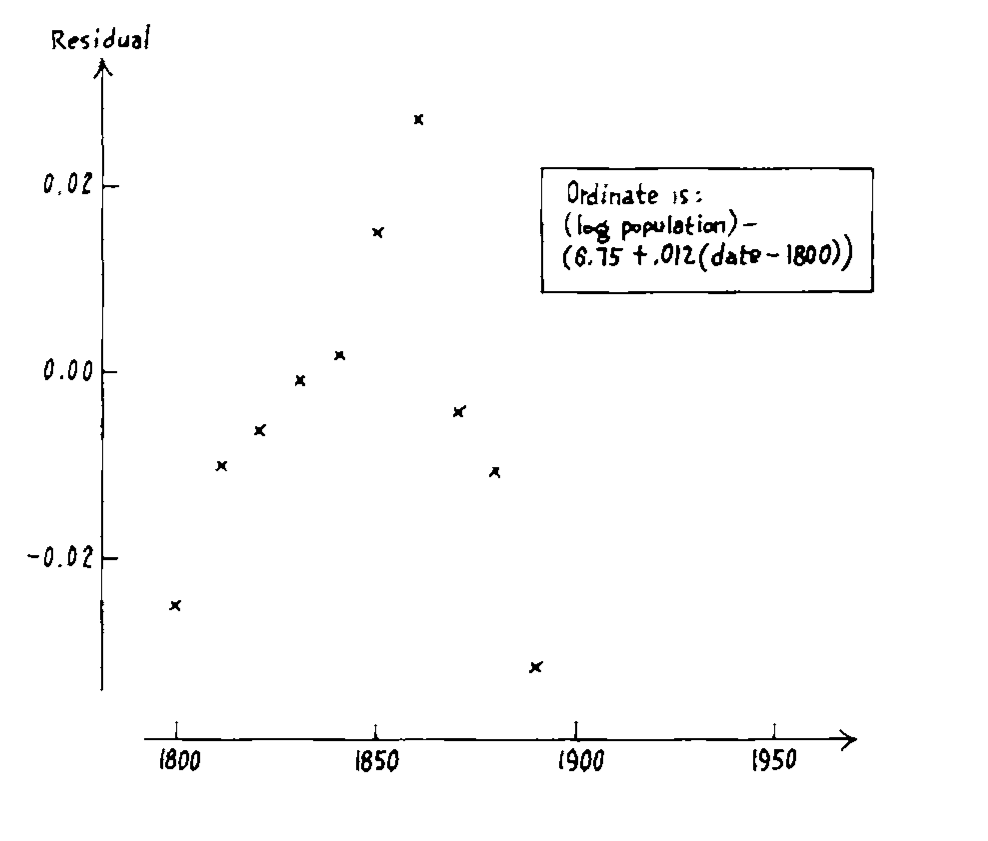
See some fluctuations in the early years, too. .monash-blue2[Note that the log transformation couldn't linearise.]
---
class: informative center middle
.outline-text[
## Whatever the data, we can try to gain by straightening or by flattening.
## When we succeed in doing one or both, we almost always see more clearly what is going on.
]
---
# Rules and advice
.pull-left[
.font_medium2[
1.Graphics are friendly.
2.Arithmetic often exists to make graphs possible.
3..monash-orange2[Graphs force us to note the unexpected]; nothing could be more important.
4.Different graphs show us quite different aspects of the same data.
5.There is .monash-orange2[no more reason to expect one graph to "tell all"] than to expect one number to do the same.
6."Plotting $y$ against $x$" involves significant choices--how we express one or both variables can be crucial.
]]
--
.pull-right[
.font_smaller[
7.The first step in penetrating plotting is to straighten out the dependence or point scatter as much as reasonable.
8.Plotting $y^2$, $\sqrt{y}$, $log(y)$, $-1/y$ or the like instead of $y$ is one plausible step to take in search of straightness.
9.Plotting $x^2$, $\sqrt{x}$, $log(x)$, $-1/x$ or the like instead of $x$ is another.
10.Once the plot is straightened, we can usually gain much by flattening it, usually by plotting residuals.
11.When plotting scatters, we may need to be careful about how we express $x$ and $y$ in order to avoid concealment by crowding.
]]
---
class: middle
background-image: \url(https://vignette.wikia.nocookie.net/starwars/images/d/d6/Yoda_SWSB.png/revision/latest?cb=20150206140125)
background-size: cover
.monash-white[The book is a digest of] `r emo::ji("star")` .monash-white[tricks and treats] `r emo::ji("star")` .monash-white[of massaging numbers and drafting displays.]
.monash-white[Many of the tools have made it into today's analyses in various ways. Many have not.]
.monash-white[Notice the word developments too:] .monash-pink2[froots, fences]. .monash-white[Tukey brought you the word] .monash-pink2["software"].monash-white[!]
.monash-white[The temperament of the book is an inspiration for the mind-set for this unit. There is such delight in working with numbers!]
`r anicon::nia("We love data!", animate="spin", anitype="hover", colour="yellow", size="2")`
---
# Resources
- [wikipedia](https://en.wikipedia.org/wiki/Exploratory_data_analysis)
- John W. Tukey (1977) Exploratory data analysis
- Data coding using [`tidyverse` suite of R packages](https://www.tidyverse.org)
- Sketching canvases made using [`fabricerin`](https://ihaddadenfodil.com/post/fabricerin-a-tutorial/)
- Slides constructed with [`xaringan`](https://github.com/yihui/xaringan), [remark.js](https://remarkjs.com), [`knitr`](http://yihui.name/knitr), and [R Markdown](https://rmarkdown.rstudio.com).
---
```{r endslide, child="assets/endslide.Rmd"}
```
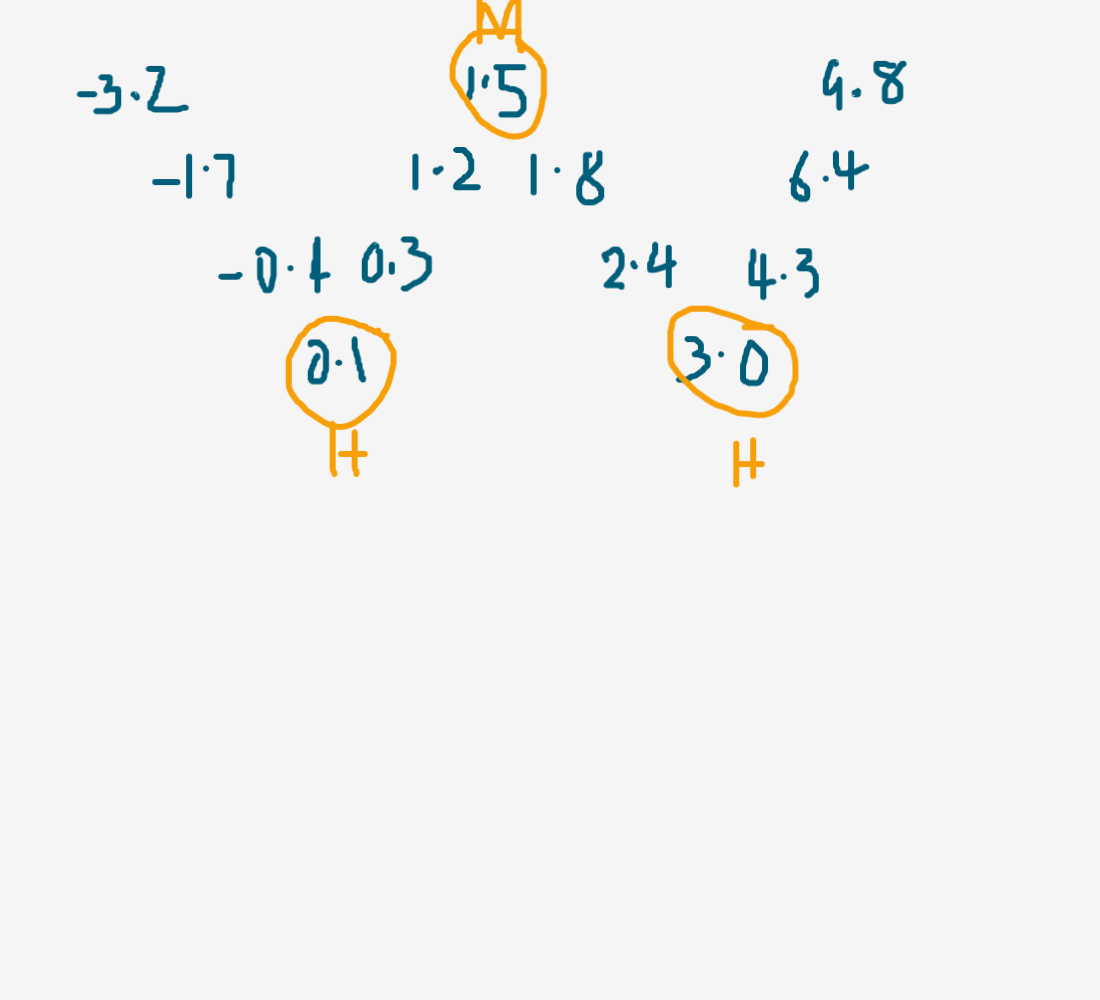 ]
.pull-right[
]
.pull-right[
 ]
hinges are alternatively known as Q1 and Q3.
---
# box-and-whisker display
.pull-left[
]
hinges are alternatively known as Q1 and Q3.
---
# box-and-whisker display
.pull-left[
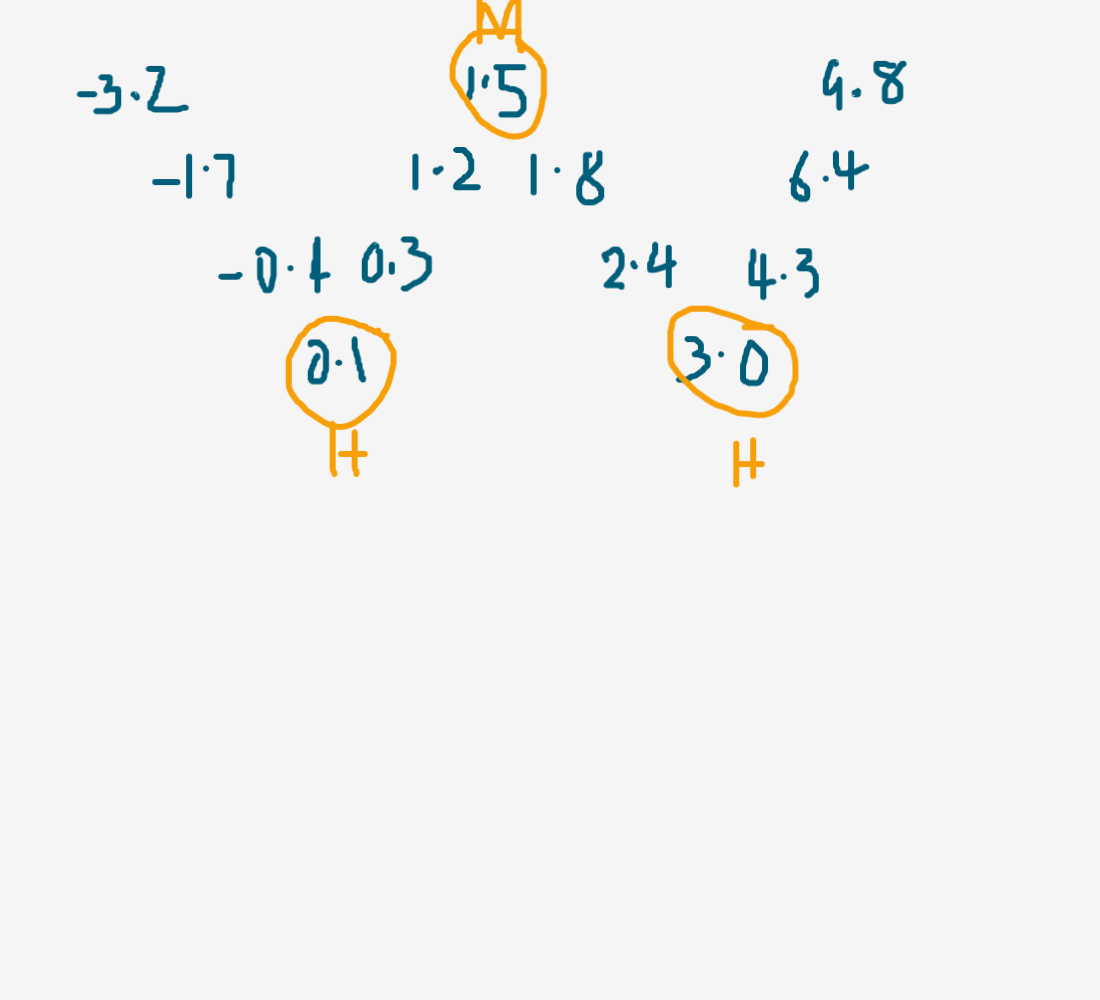 ]
.pull-right[
Starting with a 5-number summary
]
.pull-right[
Starting with a 5-number summary
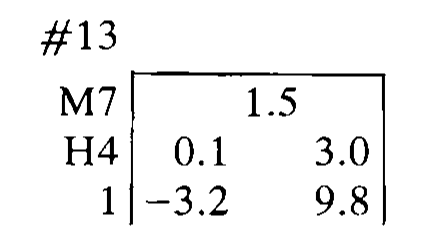 ]
---
# box-and-whisker display
.pull-left[
Starting with a 5-number summary
]
---
# box-and-whisker display
.pull-left[
Starting with a 5-number summary
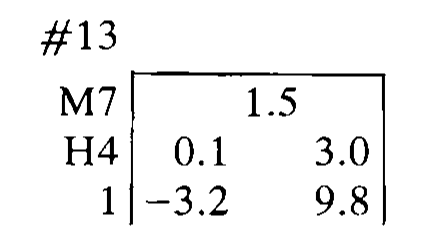 ]
.pull-right[
```{r}
fabric_drawing(cid = "canvas4",
cwidth = 550,
cheight = 500,
cfill = "whitesmoke",
drawingWidth = 3,
gumSize = 10)
```
]
---
# Identified end values
.pull-left[
]
.pull-right[
```{r}
fabric_drawing(cid = "canvas4",
cwidth = 550,
cheight = 500,
cfill = "whitesmoke",
drawingWidth = 3,
gumSize = 10)
```
]
---
# Identified end values
.pull-left[
 Why are some individual points singled out?
]
.pull-right[
Why are some individual points singled out?
]
.pull-right[
 Rules for this one may be clearer?
]
---
class: motivator middle center
## `r emo::ji("scream_cat")` Isn't this imposing a belief?
---
class: middle center
.outline-text[## There is no excuse for failing to plot and look]
Rules for this one may be clearer?
]
---
class: motivator middle center
## `r emo::ji("scream_cat")` Isn't this imposing a belief?
---
class: middle center
.outline-text[## There is no excuse for failing to plot and look]
 .monash-orange2[How would you make an 11-number summary?]
]
.pull-right[
.font_smaller[
```{r lvplot, echo=TRUE}
library(lvplot)
p <- ggplot(mpg,
aes(class, hwy))
p + geom_lv(aes(fill=..LV..)) + #<<
scale_fill_brewer()
```
]
]
---
class: informative middle
## Box plots are ubiquitous in use today.
`r emo::ji("dog")` `r emo::ji("cat")` Mostly used to compare distributions, multiple subsets of the data.
Puts the emphasis on the `r anicon::nia("middle 50%", animate="spin", anitype="hover", color="yellow")` of observations, although variations can put emphasis on other aspects.
---
class: transition middle animated slideInLeft
## Easy re-expression
---
# Logs, square roots, reciprocals
.pull-left[
What you need to know about logs?
- how to find good enough logs fast and easily
- that equal differences in logs correspond to equal ratios of raw values. .font_smaller[(This means that wherever you find people using products or ratios-- even in such things as price indexes--using logs--thus converting producers to sums and ratios to differences--is likely to help.)]
]
--
.pull-right[
The most common transformations are logs, sqrt root, reciprocals, reciprocals of square roots
.monash-orange2[How would you make an 11-number summary?]
]
.pull-right[
.font_smaller[
```{r lvplot, echo=TRUE}
library(lvplot)
p <- ggplot(mpg,
aes(class, hwy))
p + geom_lv(aes(fill=..LV..)) + #<<
scale_fill_brewer()
```
]
]
---
class: informative middle
## Box plots are ubiquitous in use today.
`r emo::ji("dog")` `r emo::ji("cat")` Mostly used to compare distributions, multiple subsets of the data.
Puts the emphasis on the `r anicon::nia("middle 50%", animate="spin", anitype="hover", color="yellow")` of observations, although variations can put emphasis on other aspects.
---
class: transition middle animated slideInLeft
## Easy re-expression
---
# Logs, square roots, reciprocals
.pull-left[
What you need to know about logs?
- how to find good enough logs fast and easily
- that equal differences in logs correspond to equal ratios of raw values. .font_smaller[(This means that wherever you find people using products or ratios-- even in such things as price indexes--using logs--thus converting producers to sums and ratios to differences--is likely to help.)]
]
--
.pull-right[
The most common transformations are logs, sqrt root, reciprocals, reciprocals of square roots
 ---
class: center middle
## Power ladder
---
class: center middle
## Power ladder





