## `r emo::ji("target")` Objectives
These are exercises in plots to make to explore relationships between multiple variables. You will use interactive scatterplot matrices, interactive parallel coordinate plots and tours to explore the world beyond 2D.
## `r emo::ji("wrench")` Preparation
- The reading for this week is [Cook and Laa (2023) "Interactively exploring high-dimensional data and models in R" Chapter 1](https://dicook.github.io/mulgar_book/1-intro.html).
- Complete the weekly quiz, before the deadline!
- Install the following R-packages if you do not have them already:
```{r}
#| eval: false
#| code-fold: false
install.packages(c("tidyverse", "cassowaryr", "tourr", "GGally", "plotly", "colorspace", "SMPracticals", "vcdExtra", "patchwork", "vcd"))
```
- Open your RStudio Project for this unit, (the one you created in week 1, `eda` or `ETC5521`).
```{r libraries}
#| message: false
#| echo: false
library(tidyverse)
library(GGally)
library(tourr)
library(cassowaryr)
library(plotly)
library(colorspace)
library(patchwork)
library(vcd)
theme_set(ggthemes::theme_gdocs(base_size = 12) +
theme(
plot.background = element_rect(fill = "transparent", colour = NA),
axis.line.x = element_line(color = "black", linetype = "solid"),
axis.line.y = element_line(color = "black", linetype = "solid"),
#plot.title.position = "plot",
#plot.title = element_text(size = 24),
panel.background = element_rect(fill = "transparent", colour = "black"),
panel.grid.major = element_blank(),
legend.background = element_rect(fill = "transparent", colour = NA),
legend.key = element_rect(fill = "transparent", colour = NA)
))
```
## Exercise 1: Melbourne housing
a. Read in a copy of the Melbourne housing data from [Nick Tierney's github repo](https://github.com/njtierney/melb-housing-data) which is a collation from the version at [kaggle](https://www.kaggle.com/anthonypino/melbourne-housing-market/version/21). Its fairly large, so let's start simply, and choose two suburbs to focus on. I recommend "South Yarra" and "Brighton". (Note: there are a number of missing values. I recommend removing these before making plots.)
```{r}
#| label: read-houses
#| message: false
mel_houses <- read_csv("https://raw.githubusercontent.com/njtierney/melb-housing-data/master/data/housing.csv") %>%
dplyr::filter(suburb %in% c("South Yarra", "Brighton")) %>%
dplyr::filter(!is.na(bedroom2)) %>%
dplyr::filter(!is.na(bathroom)) %>%
dplyr::filter(!is.na(price))
```
b. Make a scatterplot matrix of price, rooms, bedroom2, bathroom, suburb, type. The order of variables can affect the readability. I advise that the plot will be easier to read if you order them with the numerical variables first, and then the categorical variables. Think about what associations can be seen?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 8
#| message: false
ggpairs(mel_houses, columns=c(4,2,10,11,1,3))
```
- Except for price the continuous variables are all discrete. We can still examine the associations. It could be useful to use a jittered scatterplot, but that would require making a special plot function to use in the ggpairs function.
- There is positive linear association between price, rooms, bedroom2, bathroom, which indicates the bigger the house the higher the price
- From the boxplots: houses in Brighton tend to be higher priced and bigger than South Yarra, and houses tend to be worth more than apartments or units.
- From the fluctuation diagram, Brighton tends to have more houses, and South Yarra has more apartments.
- From the density plot, price has a skewed distribution.
- There is one big outlier, one house sold for a much higher price. There are a few bivariate outliers, houses with a large number of bathrooms but relatively low price.
```{r}
#| eval: false
#| message: false
# To add jitter
ggpairs(mel_houses, columns=c(4,2,10,11,1,3),
lower=list(continuous=wrap("points",
position=position_jitter(height=0.3, width=0.3))))
```
:::
c. Subset the data to South Yarra only. Make an interactive scatterplot matrix of rooms, bedroom2, bathroom and price, coloured by type of property. There is a really high price property. Select this case, and determine what's special about it -- why did it sell for so much? Select the outlier in bedrooms and bathrooms, and examine the other characteristics of this property.
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 6
#| message: false
south_yarra <- mel_houses %>%
dplyr::filter(suburb=="South Yarra") %>%
dplyr::select(rooms, bedroom2, bathroom, price, type)
highlight_key(south_yarra) %>%
ggpairs(aes(color = type), columns = c(4,2,1,3),
upper=list(continuous="points")) %>%
ggplotly() %>%
highlight("plotly_selected")
```
This property that has a high price has relatively modest characteristics! It has 4 bedrooms and 2 bathrooms.
```{r}
#| eval: false
# To add jittering
highlight_key(south_yarra) %>%
ggpairs(aes(color = type),
columns = c(4,2,1,3),
lower=list(continuous=wrap("points",
position=position_jitter(height=0.3, width=0.3))),
upper=list(continuous=wrap("points",
position=position_jitter(height=0.3, width=0.3)))) %>%
ggplotly() %>%
highlight("plotly_selected")
```
:::
## Exercise 2: Olive oils
Following on from the olive oils example from lecture, we will explore the oils from the south here.
a. Grab a copy of the data, and subset to contain just the samples from region = south (1), and also drop eicosenoic acid, because there is nothing useful about this variable for the southern oils.
```{r olive}
#| label: read-olive
#| message: false
# Read data and filter to just south
olive <- read_csv("http://ggobi.org/book/data/olive.csv") %>%
rename(id = `...1`) %>%
dplyr::filter(region == 1) %>%
dplyr::select(palmitic:arachidic, id, area) %>%
mutate(area = factor(area))
#mutate(area = as.integer(area))
```
b. Only looking at areas (1-3), that is not Sicily:
- Make an interactive parallel coordinate plot of the fatty acids (except eicosenoic), where the lines are coloured by area. (Code is provided, code is a bit tricky, but worth it!)
- Look at the data in a tour.
- Describe what you learn about differences between the three areas, whether these are separated. Are some variables more useful for distinguishing the three areas? Are there any outliers?
```{r}
#| label: pcp-nosicily
#| eval: false
# Look at first three areas, first
not_sicily <- olive %>%
filter(area != 4)
# Set our colours for the par coords, and also tour
clrs <- divergingx_hcl(palette="Zissou 1", n=4)
# Make the interactive parcoords with plotly
# SOME NOTES ABOUT THE CODE:
# - Notice that some variables have been flipped by
# putting a minus sign in front, this is to make
# the correlation between variables positive, making
# the par coords easier to read.
# - Note the strange colour mapping: colour value has
# to range between 0-1 weirdly enough, so
# area 1 becomes 0, area 3 becomes 1
# - The range of each variable needs to be stated
# so that each is scaled from min to max for the display
# ABOUT THE INTERACTIVITY
# - Click and drag along an axis to select observations
# - Click and drag the variable label to re-order
# I find the best order to see groups is palmitoleic,
# oleic, palmitic, linoleic,
# linolenic, arachidic, stearic
not_sicily_pcp <- not_sicily %>%
plot_ly(type = 'parcoords',
line = list(color = ~area,
colorscale = list(c(0,clrs[1]), c(0.5,clrs[2]),
c(1,clrs[3]))),
dimensions = list(
list(range = c(35,280),
label = 'palmitoleic', values = ~palmitoleic),
list(range = c(-8113,-6300),
label = 'oleic', values = ~(-oleic)),
list(range = c(875,1753),
label = 'palmitic', values = ~palmitic),
list(range = c(448,1462),
label = 'linoleic', values = ~linoleic),
list(range = c(-74,-20),
label = 'linolenic', values = ~(-linolenic)),
list(range = c(-102,-32),
label = 'arachidic', values = ~(-arachidic)),
list(range = c(-375,-152),
label = 'stearic', values = ~(-stearic))
)
)
not_sicily_pcp
```
To generate a tour use:
```{r}
#| label: tour-nosicily
#| eval: false
animate_xy(not_sicily[,1:7], col=not_sicily$area, rescale=TRUE)
```
::: unilur-solution
```{r}
#| label: pcp-nosicily
#| echo: false
```
The three areas are quite different on a combination of palmitoleic, oleic, palmitic, and linoleic acids. There are some possible outliers, that can be found by selecting various lines, and noticing that it has a different trend than other lines.
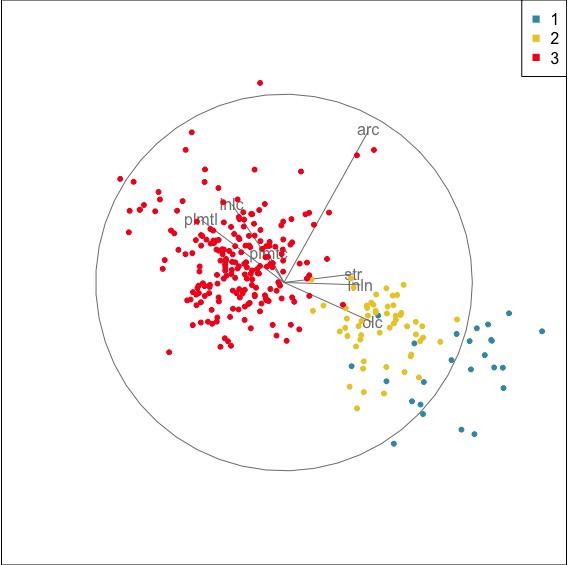 The three areas are quite distinct. We could distinguish the growing area of the olive oils by examining the fatty acid composition.
:::
c. Re-do b. with Sicily. Explain what you learn about Sicily relative to the other areas.
::: unilur-solution
```{r}
#| label: pcp-all
# Now all four area
olive_pcp <- olive %>%
plot_ly(type = 'parcoords',
line = list(color = ~area,
colorscale = list(c(0,clrs[1]), c(0.33,clrs[2]),
c(0.67,clrs[3]), c(1,clrs[4]))),
dimensions = list(
list(range = c(35,280),
label = 'palmitoleic', values = ~palmitoleic),
list(range = c(-8113,-6300),
label = 'oleic', values = ~(-oleic)),
list(range = c(875,1753),
label = 'palmitic', values = ~palmitic),
list(range = c(448,1462),
label = 'linoleic', values = ~linoleic),
list(range = c(-74,-20),
label = 'linolenic', values = ~(-linolenic)),
list(range = c(-102,-32),
label = 'arachidic', values = ~(-arachidic)),
list(range = c(-375,-152),
label = 'stearic', values = ~(-stearic))
)
)
olive_pcp
```
```{r}
#| eval: false
animate_xy(olive[,1:7], col=olive$area, rescale=TRUE)
```
The three areas are quite distinct. We could distinguish the growing area of the olive oils by examining the fatty acid composition.
:::
c. Re-do b. with Sicily. Explain what you learn about Sicily relative to the other areas.
::: unilur-solution
```{r}
#| label: pcp-all
# Now all four area
olive_pcp <- olive %>%
plot_ly(type = 'parcoords',
line = list(color = ~area,
colorscale = list(c(0,clrs[1]), c(0.33,clrs[2]),
c(0.67,clrs[3]), c(1,clrs[4]))),
dimensions = list(
list(range = c(35,280),
label = 'palmitoleic', values = ~palmitoleic),
list(range = c(-8113,-6300),
label = 'oleic', values = ~(-oleic)),
list(range = c(875,1753),
label = 'palmitic', values = ~palmitic),
list(range = c(448,1462),
label = 'linoleic', values = ~linoleic),
list(range = c(-74,-20),
label = 'linolenic', values = ~(-linolenic)),
list(range = c(-102,-32),
label = 'arachidic', values = ~(-arachidic)),
list(range = c(-375,-152),
label = 'stearic', values = ~(-stearic))
)
)
olive_pcp
```
```{r}
#| eval: false
animate_xy(olive[,1:7], col=olive$area, rescale=TRUE)
```
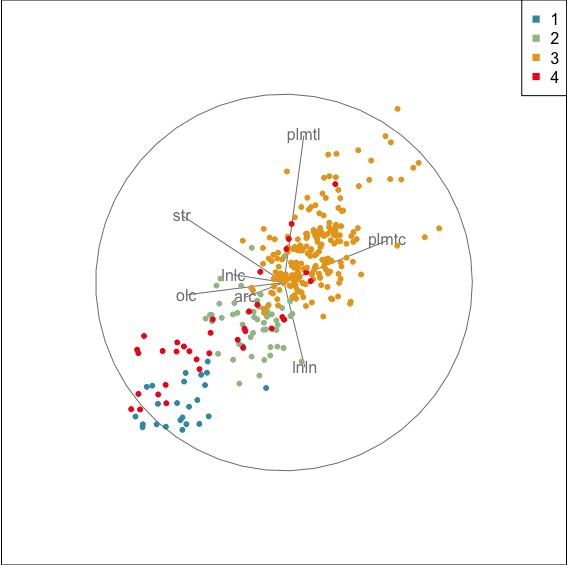 Sicily overlaps with two of the other three areas. Most of the samples are not distinguishable from the other two.
:::
d. Use your AI helper or do some googling. What can you find out about Sicilian olive oils? Are they higher in value? Does Sicily even grow olives, or does it use olives from neighbouring areas?
::: unilur-solution
Not sure what the reason is! Maybe growing conditions in some fields are similar in the three areas. Probably the best explanation is that Sicily imports olives from neighbouring areas to make the oils.
:::
## Exercise 3: Baker field soils
The data measures essential elements in the soils for agricultural uses in the Baker field in Iowa. Some of these variables are skewed, which makes examining associations between them and other variables less useful. It can help to transform skewed variables to be more symmetric and then check for associations. This is what we will do here.
```{r}
#| label: corn
#| message: false
corn <- read_csv("https://eda.numbat.space/data/baker.csv")
```
a. Make density plots of the soil variables in the Baker field corn yield data. Choose an appropriate transformation to symmetrise the distribution.
::: unilur-solution
Many of the variables have a right-skewed distribution. For this thinking about a square root or log transformation would be appropriate. Ca has a severe right-skew, so a log-log transformation might be required. The code below shows the transformations made.
```{r}
corn_long <- corn %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
corn_trf <- corn %>%
mutate(B = log10(B),
Ca = log10(log10(Ca)),
Cu = sqrt(Cu),
K = log10(K),
Mg = sqrt(Mg),
Mn = sqrt(Mn),
Na = sqrt(Na),
P = log10(P),
Zn = sqrt(Zn))
corn_long <- corn_trf %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
```
The transformed data has mostly symmetric, unimodal distributions now. Making these transformations is useful when considering the relationship between variables. If each variable is well-spread then the association is measured using most of the points, but if you try to assess the association between skewed distributions, the judgement is based on just a handful of observations.
:::
b. Examine the pairwise associations using an interactive scatterplot matrix. Describe what you learn.
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 8
#| message: false
highlight_key(corn_trf) %>%
ggpairs(columns=4:13) %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Strong positive linear association: eg Ca-Cu, K-P
- Weak negative linear association: Fe-Ca
- Potential outliers: univariate Na; bivariate Ca-Cu
- Nonlinear association: Fe-Cu
I don't know what these mean, but the non-linear relationship is interesting.
When Fe is low,
- Cu is high, then Ca and other variables like Mg are high.
- Cu is low, then Ca and other variables like Mg are low
When Fe is high, the relationship between Ca and Cu (and Ca-Mg) is very strongly positive.
:::
c. Using a grand tour, how would you answer the following questions? Is there clustering? Is there linear dependence? Non-linear dependence? outliers. For any structure that you see determine which variables contribute to it, and make plots of these variables (or check the scatterplot matrix) to check whether the pattern is visible there too.
::: unilur-solution
```{r}
#| eval: false
animate_xy(corn_trf[,4:13], rescale = TRUE)
```
Sicily overlaps with two of the other three areas. Most of the samples are not distinguishable from the other two.
:::
d. Use your AI helper or do some googling. What can you find out about Sicilian olive oils? Are they higher in value? Does Sicily even grow olives, or does it use olives from neighbouring areas?
::: unilur-solution
Not sure what the reason is! Maybe growing conditions in some fields are similar in the three areas. Probably the best explanation is that Sicily imports olives from neighbouring areas to make the oils.
:::
## Exercise 3: Baker field soils
The data measures essential elements in the soils for agricultural uses in the Baker field in Iowa. Some of these variables are skewed, which makes examining associations between them and other variables less useful. It can help to transform skewed variables to be more symmetric and then check for associations. This is what we will do here.
```{r}
#| label: corn
#| message: false
corn <- read_csv("https://eda.numbat.space/data/baker.csv")
```
a. Make density plots of the soil variables in the Baker field corn yield data. Choose an appropriate transformation to symmetrise the distribution.
::: unilur-solution
Many of the variables have a right-skewed distribution. For this thinking about a square root or log transformation would be appropriate. Ca has a severe right-skew, so a log-log transformation might be required. The code below shows the transformations made.
```{r}
corn_long <- corn %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
corn_trf <- corn %>%
mutate(B = log10(B),
Ca = log10(log10(Ca)),
Cu = sqrt(Cu),
K = log10(K),
Mg = sqrt(Mg),
Mn = sqrt(Mn),
Na = sqrt(Na),
P = log10(P),
Zn = sqrt(Zn))
corn_long <- corn_trf %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
```
The transformed data has mostly symmetric, unimodal distributions now. Making these transformations is useful when considering the relationship between variables. If each variable is well-spread then the association is measured using most of the points, but if you try to assess the association between skewed distributions, the judgement is based on just a handful of observations.
:::
b. Examine the pairwise associations using an interactive scatterplot matrix. Describe what you learn.
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 8
#| message: false
highlight_key(corn_trf) %>%
ggpairs(columns=4:13) %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Strong positive linear association: eg Ca-Cu, K-P
- Weak negative linear association: Fe-Ca
- Potential outliers: univariate Na; bivariate Ca-Cu
- Nonlinear association: Fe-Cu
I don't know what these mean, but the non-linear relationship is interesting.
When Fe is low,
- Cu is high, then Ca and other variables like Mg are high.
- Cu is low, then Ca and other variables like Mg are low
When Fe is high, the relationship between Ca and Cu (and Ca-Mg) is very strongly positive.
:::
c. Using a grand tour, how would you answer the following questions? Is there clustering? Is there linear dependence? Non-linear dependence? outliers. For any structure that you see determine which variables contribute to it, and make plots of these variables (or check the scatterplot matrix) to check whether the pattern is visible there too.
::: unilur-solution
```{r}
#| eval: false
animate_xy(corn_trf[,4:13], rescale = TRUE)
```
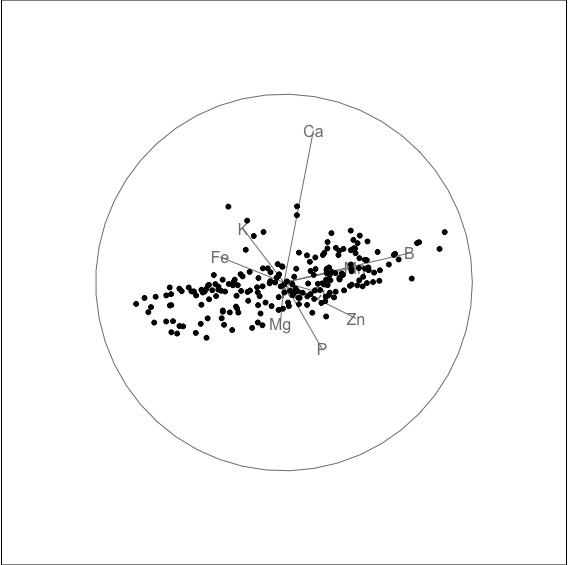
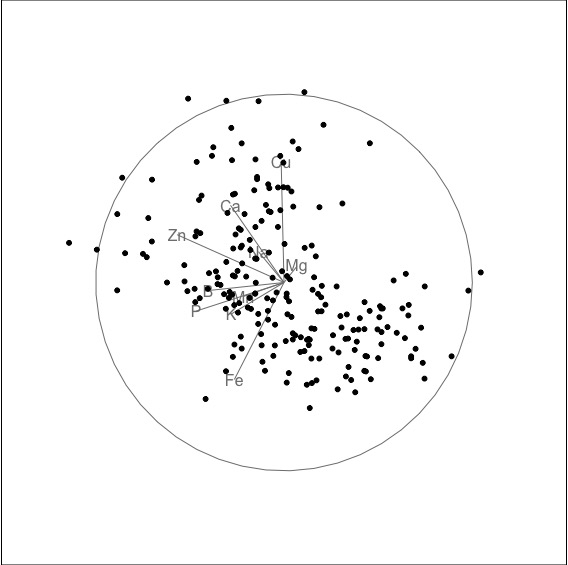
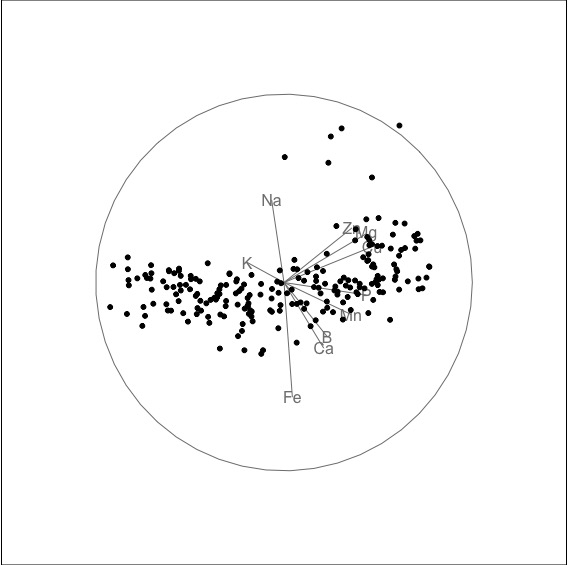 - There is no clustering.
- There is linear dependence, quite strong.
- There is a small amount of non-linear dependence.
- There are some outliers. See third snapshot above, to see non-linear dependence and outliers, when primarily Fe and Na are combined. This was not visible in the pairwise plot.
:::
## Exercise 4: Exam marks
There is a dataset `mathmarks` in the SMPracticals package, which has marks out of 100 for 88 students. It is interesting to note that all students had marks for all tests, which makes one wonder whether marks for students who missed a test were dropped. Mechanics and vectors were closed book exams, and the others were open book.
```{r math}
#| label: math
data(mathmarks, package="SMPracticals")
```
a. Make a side-by-side boxplot of the test scores. What do you learn about the test scores on the different subjects?
::: unilur-solution
```{r}
mathmarks %>%
pivot_longer(everything(), names_to="var", values_to="marks") %>%
mutate(var = factor(var, levels=unique(var))) %>%
ggplot(aes(x=var, y=marks)) +
geom_boxplot()
```
There is some difference in median and IQR across exams. Students tended to do better on vectors, algebra and analysis and worse on mechanics and statistics. There is no indication that the open book exams produced better scores than the closed book exams.
The distributions are fairly symmetric. The spread is similar except for algebra which are more concentrated. There is one quite high score on algebra, and two low scores. Mechanics and vectors has an unusually low score each.
:::
b. Make a scatterplot matrix, even better if it is interactive. Describe the relationships between the tests. Is there something different about the open book vs closed book scores?
::: unilur-solution
```{r}
#| message: false
#| fig-width: 8
#| fig-height: 8
highlight_key(mathmarks) %>%
ggpairs() %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Generally we can see positive linear association. Algebra and analysis are most related. Algebra is pretty closely related to all other test scores. Mechanics is only weakly related to statistics.
- There are a couple of outliers: low scores on algebra, and also two students who did badly on vectors but quite well on analysis.
- There looks to be a barrier at 80 for the statistics test, maybe this was the maximum possible score.
- Analysis and algebra, and also analysis and vectors has what I call a "comet" distribution: there is a tight concentration of high scores, and a big spread among lower scores. I see this a lot in statistics test scores.
:::
c. Make an interactive parallel coordinate plot. Are there some students who have done consistently well on all tests? Consistently badly on all tests? Badly on some but better on others?
::: unilur-solution
```{r}
marks_pcp <- mathmarks %>%
plot_ly(type = 'parcoords',
dimensions = list(
list(range = c(0,100),
label = 'mechanics', values = ~mechanics),
list(range = c(0,100),
label = 'vectors', values = ~vectors),
list(range = c(0,100),
label = 'algebra', values = ~algebra),
list(range = c(1,100),
label = 'analysis', values = ~analysis),
list(range = c(1,100),
label = 'statistics', values = ~statistics)
)
)
marks_pcp
```
- There is one student who did poorly on the closed book exams, but relatively better on the open book exams.
- There is one student who did really well on the closed book vectors exam, but badly on all other exams.
- There are a few students who have done really well on all exams.
- Generally, a student does relatively as well across all the tests. - There appears to be some slight bimodality or multimodality in mechanics, analysis and statistics which is also visible in the density plots in the splom.
:::
## Exercise 5: Knowledge and resources
The `vcdExtra` package contains a dataset `Dyke` about how 1729 survey respondents' knowledge of cancer depended on whether they listened to the radio, read newspapers, did solid reading, or attended lectures. This data is all categorical, so we need to make plots to show the relationships between five categorical variables.
```{r}
data(Dyke, package="vcdExtra")
```
a. Make separate bar charts for each of the explanatory variables, with bars filled by the response variable `Knowledge`. What do you learn?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
Dyke_tsb <- as_tibble(Dyke) %>%
mutate(Knowledge = factor(Knowledge, levels=c("Good", "Poor")),
Reading = factor(Reading, levels=c("Yes", "No")),
Radio = factor(Radio, levels=c("Yes", "No")),
Lectures = factor(Lectures, levels=c("Yes", "No")),
Newspaper = factor(Newspaper, levels=c("Yes", "No")))
p1 <- ggplot(Dyke_tsb, aes(x=Reading, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p2 <- ggplot(Dyke_tsb, aes(x=Radio, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
scale_fill_discrete_divergingx(palette="Zissou 1")
p3 <- ggplot(Dyke_tsb, aes(x=Lectures, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p4 <- ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p1 + p2 + p3 + p4 + plot_layout(ncol=4,
guides="collect") &
theme(legend.position = "bottom", legend.direction = "horizontal")
```
The focus here is on counts, and it is hard to read proportions. We learn that there are
- roughly equal numbers of Yes/No in Reading, and similarly in Newspaper.
- but much fewer people listen to the Radio or attend Lectures.
:::
b. Make a 100% bar chart of Newspaper, with Knowledge mapped to fill, and faceted by Reading. What do you learn about the relative proportions in the groups?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_bar(stat="identity",
position = position_fill(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1") +
facet_wrap(~Reading, labeller=labeller(Reading=label_both))
```
- When Reading is Yes, Knowledge is more likely to be good, than if Reading is No.
- When Newspaper is Yes, in both Reading Yes and No, Knowledge is more likely to be Good, then if Newspaper is No.
:::
c. Make a doubledecker plot of the data. What combination of factors leads to the highest level of knowledge about cancer? What combination leads to the lowest?
```{r}
#| echo: true
#| eval: false
#| label: knowledge-dd
# I had a difficult time getting the Good category being the first
# and to be coloured red, but this appears to work
Dyke_tbl <- Dyke_tsb %>%
mutate(Knowledge = factor(Knowledge, levels=c("Poor", "Good"))) %>%
uncount(n) %>%
select(Reading, Radio, Lectures, Newspaper, Knowledge) %>%
arrange(Knowledge, Reading, Radio, Lectures, Newspaper)
doubledecker(Knowledge~., Dyke_tbl,
gp = gpar(fill=c("grey90", "orangered")))
```
::: unilur-solution
```{r}
#| echo: false
#| eval: true
#| label: knowledge-dd
```
From the double-decker plot, it is much easier to read off which combinations of factors yields the higher knowledge.
The most knowledgeable people read, listen to the radio, attend lectures and read newspapers - as might be expected. There a very few people in this category, though. On each comparison the Yes group is more knowledgeable than the No group. The most populous group is the No to all combination. This is pretty shocking because it is the least knowledgeable about cancer. The second most common group are people who read newspapers, and read generally, and these are relatively knowledgeable about cancer.
:::
## Exercise 6: Parkinsons
This dataset is composed of a range of biomedical voice measurements from 31 people, 23 with Parkinson's disease (PD). Each column in the table is a particular voice measure, and each row corresponds one of 195 voice recording from these individuals ("name" column). The main aim of the data is to discriminate healthy people from those with PD, according to "status" column which is set to 0 for healthy and 1 for PD.
The data is available at [The UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Parkinsons) in ASCII CSV format. The rows of the CSV file contain an instance corresponding to one voice recording. There are around six recordings per patient, the name of the patient is identified in the first column. There are 24 variables in the file, including the persons name in column 1.
The data are originally analysed in:
Max A. Little, Patrick E. McSharry, Eric J. Hunter, Lorraine O. Ramig (2008), 'Suitability of dysphonia measurements for telemonitoring of Parkinson's disease', IEEE Transactions on Biomedical Engineering (to appear).
```{r}
#| eval: true
#| echo: true
library(cassowaryr)
# Load the data
data(pk)
```
a. How many pairwise plots would you need to look at, to look at all of them?
::: unilur-solution
There are 23 numeric variables in the data set, which would require `r 23*22/2` pairwise plots to be made.
:::
b. Compute several of the scagnostics (monotonic, outlying, clumpy2) for the first five variables of variables, except for `name`. (*Note*: We are using just five for computing speed, but the scagnostics could be calculated on all variables.)
```{r}
#| eval: false
#| echo: true
#| label: pk
# Compute the scagnostics on the relevant variables
s <- calc_scags_wide(pk[,2:5],
scags=c("outlying","monotonic",
"clumpy2"))
s
```
::: unilur-solution
```{r}
#| eval: true
#| echo: false
#| message: false
#| label: pk
```
:::
c. Sort the scagnostics, separately by the values on (i) monotonic (ii) outlying (iii) clumpy2, and plot the pair of variables with the highest values on each.
::: unilur-solution
```{r}
# Check the results for monotonic
s %>%
select(Var1, Var2, monotonic) %>%
arrange(desc(monotonic))
ggplot(data=pk,
aes(x=`MDVP:Fhi(Hz)`, y=`MDVP:Fo(Hz)`)) +
geom_point() + theme(aspect.ratio = 1)
```
The top pair of variables on monotonic has a strong positive association with the majority of points, and a few outliers. The top pair of variables on outlying, is also the top pair on clumpy2, and has outliers with some clumpiness in the mass of points with low values.
:::
d. Make an interactive scatterplot matrix. Browse over it to choose other interesting pairs of variables and make the plots.
::: unilur-solution
```{r}
#| message: false
# Create an interactive splom
s <- s %>%
mutate(vars = paste(Var1, Var2))
highlight_key(s) %>%
GGally::ggpairs(columns = 3:5, mapping = aes(label = vars)) %>%
ggplotly(tooltip = "all",
width=500,
height=500) %>%
highlight("plotly_selected")
```
:::
e. The scagnostics help us to find interesting associations between pairs of variables. However, the problem here is to detect differences between Parkinsons patients and normal patients. How would you go about that? Think about some ideas long the line of scagnostics but look for differences between the two groups.
::: unilur-solution
```{r}
# One way to examine difference between Parkinsons and healthy
pk_med <- pk %>%
select(-name) %>%
group_by(status) %>%
summarise_all(list(median, sd)) %>%
pivot_longer(
cols=`MDVP:Fo(Hz)_fn1`:`PPE_fn2`,
names_to="var",
values_to="value") %>%
separate(var, c("var","stat"), "_") %>%
mutate(stat = fct_recode(stat,
"m"="fn1",
"s"="fn2")) %>%
pivot_wider(names_from=stat,
values_from=value) %>%
group_by(var) %>%
summarise(
d = (m[status==0]-m[status==1])/sqrt(s[status==0]^2+s[status==1]^2))
pk_med %>% arrange(desc(d)) %>% head()
ggplot(pk, aes(x=factor(status), y=`MDVP:Fo(Hz)`)) +
geom_boxplot()
```
Generally we are looking for variables where the differences between the Parkinsons and normal patients are big. You need to measure big, relative to the variance of each group. Doing a two sample t-test for each variable is one approach. Here, I've computed the median for each group of patients and compared the difference in medians relative to the pooled standard deviation in each group.
:::
## `r emo::ji("wave")` Finishing up
Make sure you say thanks and good-bye to your tutor. This is a time to also report what you enjoyed and what you found difficult.
- There is no clustering.
- There is linear dependence, quite strong.
- There is a small amount of non-linear dependence.
- There are some outliers. See third snapshot above, to see non-linear dependence and outliers, when primarily Fe and Na are combined. This was not visible in the pairwise plot.
:::
## Exercise 4: Exam marks
There is a dataset `mathmarks` in the SMPracticals package, which has marks out of 100 for 88 students. It is interesting to note that all students had marks for all tests, which makes one wonder whether marks for students who missed a test were dropped. Mechanics and vectors were closed book exams, and the others were open book.
```{r math}
#| label: math
data(mathmarks, package="SMPracticals")
```
a. Make a side-by-side boxplot of the test scores. What do you learn about the test scores on the different subjects?
::: unilur-solution
```{r}
mathmarks %>%
pivot_longer(everything(), names_to="var", values_to="marks") %>%
mutate(var = factor(var, levels=unique(var))) %>%
ggplot(aes(x=var, y=marks)) +
geom_boxplot()
```
There is some difference in median and IQR across exams. Students tended to do better on vectors, algebra and analysis and worse on mechanics and statistics. There is no indication that the open book exams produced better scores than the closed book exams.
The distributions are fairly symmetric. The spread is similar except for algebra which are more concentrated. There is one quite high score on algebra, and two low scores. Mechanics and vectors has an unusually low score each.
:::
b. Make a scatterplot matrix, even better if it is interactive. Describe the relationships between the tests. Is there something different about the open book vs closed book scores?
::: unilur-solution
```{r}
#| message: false
#| fig-width: 8
#| fig-height: 8
highlight_key(mathmarks) %>%
ggpairs() %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Generally we can see positive linear association. Algebra and analysis are most related. Algebra is pretty closely related to all other test scores. Mechanics is only weakly related to statistics.
- There are a couple of outliers: low scores on algebra, and also two students who did badly on vectors but quite well on analysis.
- There looks to be a barrier at 80 for the statistics test, maybe this was the maximum possible score.
- Analysis and algebra, and also analysis and vectors has what I call a "comet" distribution: there is a tight concentration of high scores, and a big spread among lower scores. I see this a lot in statistics test scores.
:::
c. Make an interactive parallel coordinate plot. Are there some students who have done consistently well on all tests? Consistently badly on all tests? Badly on some but better on others?
::: unilur-solution
```{r}
marks_pcp <- mathmarks %>%
plot_ly(type = 'parcoords',
dimensions = list(
list(range = c(0,100),
label = 'mechanics', values = ~mechanics),
list(range = c(0,100),
label = 'vectors', values = ~vectors),
list(range = c(0,100),
label = 'algebra', values = ~algebra),
list(range = c(1,100),
label = 'analysis', values = ~analysis),
list(range = c(1,100),
label = 'statistics', values = ~statistics)
)
)
marks_pcp
```
- There is one student who did poorly on the closed book exams, but relatively better on the open book exams.
- There is one student who did really well on the closed book vectors exam, but badly on all other exams.
- There are a few students who have done really well on all exams.
- Generally, a student does relatively as well across all the tests. - There appears to be some slight bimodality or multimodality in mechanics, analysis and statistics which is also visible in the density plots in the splom.
:::
## Exercise 5: Knowledge and resources
The `vcdExtra` package contains a dataset `Dyke` about how 1729 survey respondents' knowledge of cancer depended on whether they listened to the radio, read newspapers, did solid reading, or attended lectures. This data is all categorical, so we need to make plots to show the relationships between five categorical variables.
```{r}
data(Dyke, package="vcdExtra")
```
a. Make separate bar charts for each of the explanatory variables, with bars filled by the response variable `Knowledge`. What do you learn?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
Dyke_tsb <- as_tibble(Dyke) %>%
mutate(Knowledge = factor(Knowledge, levels=c("Good", "Poor")),
Reading = factor(Reading, levels=c("Yes", "No")),
Radio = factor(Radio, levels=c("Yes", "No")),
Lectures = factor(Lectures, levels=c("Yes", "No")),
Newspaper = factor(Newspaper, levels=c("Yes", "No")))
p1 <- ggplot(Dyke_tsb, aes(x=Reading, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p2 <- ggplot(Dyke_tsb, aes(x=Radio, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
scale_fill_discrete_divergingx(palette="Zissou 1")
p3 <- ggplot(Dyke_tsb, aes(x=Lectures, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p4 <- ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p1 + p2 + p3 + p4 + plot_layout(ncol=4,
guides="collect") &
theme(legend.position = "bottom", legend.direction = "horizontal")
```
The focus here is on counts, and it is hard to read proportions. We learn that there are
- roughly equal numbers of Yes/No in Reading, and similarly in Newspaper.
- but much fewer people listen to the Radio or attend Lectures.
:::
b. Make a 100% bar chart of Newspaper, with Knowledge mapped to fill, and faceted by Reading. What do you learn about the relative proportions in the groups?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_bar(stat="identity",
position = position_fill(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1") +
facet_wrap(~Reading, labeller=labeller(Reading=label_both))
```
- When Reading is Yes, Knowledge is more likely to be good, than if Reading is No.
- When Newspaper is Yes, in both Reading Yes and No, Knowledge is more likely to be Good, then if Newspaper is No.
:::
c. Make a doubledecker plot of the data. What combination of factors leads to the highest level of knowledge about cancer? What combination leads to the lowest?
```{r}
#| echo: true
#| eval: false
#| label: knowledge-dd
# I had a difficult time getting the Good category being the first
# and to be coloured red, but this appears to work
Dyke_tbl <- Dyke_tsb %>%
mutate(Knowledge = factor(Knowledge, levels=c("Poor", "Good"))) %>%
uncount(n) %>%
select(Reading, Radio, Lectures, Newspaper, Knowledge) %>%
arrange(Knowledge, Reading, Radio, Lectures, Newspaper)
doubledecker(Knowledge~., Dyke_tbl,
gp = gpar(fill=c("grey90", "orangered")))
```
::: unilur-solution
```{r}
#| echo: false
#| eval: true
#| label: knowledge-dd
```
From the double-decker plot, it is much easier to read off which combinations of factors yields the higher knowledge.
The most knowledgeable people read, listen to the radio, attend lectures and read newspapers - as might be expected. There a very few people in this category, though. On each comparison the Yes group is more knowledgeable than the No group. The most populous group is the No to all combination. This is pretty shocking because it is the least knowledgeable about cancer. The second most common group are people who read newspapers, and read generally, and these are relatively knowledgeable about cancer.
:::
## Exercise 6: Parkinsons
This dataset is composed of a range of biomedical voice measurements from 31 people, 23 with Parkinson's disease (PD). Each column in the table is a particular voice measure, and each row corresponds one of 195 voice recording from these individuals ("name" column). The main aim of the data is to discriminate healthy people from those with PD, according to "status" column which is set to 0 for healthy and 1 for PD.
The data is available at [The UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Parkinsons) in ASCII CSV format. The rows of the CSV file contain an instance corresponding to one voice recording. There are around six recordings per patient, the name of the patient is identified in the first column. There are 24 variables in the file, including the persons name in column 1.
The data are originally analysed in:
Max A. Little, Patrick E. McSharry, Eric J. Hunter, Lorraine O. Ramig (2008), 'Suitability of dysphonia measurements for telemonitoring of Parkinson's disease', IEEE Transactions on Biomedical Engineering (to appear).
```{r}
#| eval: true
#| echo: true
library(cassowaryr)
# Load the data
data(pk)
```
a. How many pairwise plots would you need to look at, to look at all of them?
::: unilur-solution
There are 23 numeric variables in the data set, which would require `r 23*22/2` pairwise plots to be made.
:::
b. Compute several of the scagnostics (monotonic, outlying, clumpy2) for the first five variables of variables, except for `name`. (*Note*: We are using just five for computing speed, but the scagnostics could be calculated on all variables.)
```{r}
#| eval: false
#| echo: true
#| label: pk
# Compute the scagnostics on the relevant variables
s <- calc_scags_wide(pk[,2:5],
scags=c("outlying","monotonic",
"clumpy2"))
s
```
::: unilur-solution
```{r}
#| eval: true
#| echo: false
#| message: false
#| label: pk
```
:::
c. Sort the scagnostics, separately by the values on (i) monotonic (ii) outlying (iii) clumpy2, and plot the pair of variables with the highest values on each.
::: unilur-solution
```{r}
# Check the results for monotonic
s %>%
select(Var1, Var2, monotonic) %>%
arrange(desc(monotonic))
ggplot(data=pk,
aes(x=`MDVP:Fhi(Hz)`, y=`MDVP:Fo(Hz)`)) +
geom_point() + theme(aspect.ratio = 1)
```
The top pair of variables on monotonic has a strong positive association with the majority of points, and a few outliers. The top pair of variables on outlying, is also the top pair on clumpy2, and has outliers with some clumpiness in the mass of points with low values.
:::
d. Make an interactive scatterplot matrix. Browse over it to choose other interesting pairs of variables and make the plots.
::: unilur-solution
```{r}
#| message: false
# Create an interactive splom
s <- s %>%
mutate(vars = paste(Var1, Var2))
highlight_key(s) %>%
GGally::ggpairs(columns = 3:5, mapping = aes(label = vars)) %>%
ggplotly(tooltip = "all",
width=500,
height=500) %>%
highlight("plotly_selected")
```
:::
e. The scagnostics help us to find interesting associations between pairs of variables. However, the problem here is to detect differences between Parkinsons patients and normal patients. How would you go about that? Think about some ideas long the line of scagnostics but look for differences between the two groups.
::: unilur-solution
```{r}
# One way to examine difference between Parkinsons and healthy
pk_med <- pk %>%
select(-name) %>%
group_by(status) %>%
summarise_all(list(median, sd)) %>%
pivot_longer(
cols=`MDVP:Fo(Hz)_fn1`:`PPE_fn2`,
names_to="var",
values_to="value") %>%
separate(var, c("var","stat"), "_") %>%
mutate(stat = fct_recode(stat,
"m"="fn1",
"s"="fn2")) %>%
pivot_wider(names_from=stat,
values_from=value) %>%
group_by(var) %>%
summarise(
d = (m[status==0]-m[status==1])/sqrt(s[status==0]^2+s[status==1]^2))
pk_med %>% arrange(desc(d)) %>% head()
ggplot(pk, aes(x=factor(status), y=`MDVP:Fo(Hz)`)) +
geom_boxplot()
```
Generally we are looking for variables where the differences between the Parkinsons and normal patients are big. You need to measure big, relative to the variance of each group. Doing a two sample t-test for each variable is one approach. Here, I've computed the median for each group of patients and compared the difference in medians relative to the pooled standard deviation in each group.
:::
## `r emo::ji("wave")` Finishing up
Make sure you say thanks and good-bye to your tutor. This is a time to also report what you enjoyed and what you found difficult.
 The three areas are quite distinct. We could distinguish the growing area of the olive oils by examining the fatty acid composition.
:::
c. Re-do b. with Sicily. Explain what you learn about Sicily relative to the other areas.
::: unilur-solution
```{r}
#| label: pcp-all
# Now all four area
olive_pcp <- olive %>%
plot_ly(type = 'parcoords',
line = list(color = ~area,
colorscale = list(c(0,clrs[1]), c(0.33,clrs[2]),
c(0.67,clrs[3]), c(1,clrs[4]))),
dimensions = list(
list(range = c(35,280),
label = 'palmitoleic', values = ~palmitoleic),
list(range = c(-8113,-6300),
label = 'oleic', values = ~(-oleic)),
list(range = c(875,1753),
label = 'palmitic', values = ~palmitic),
list(range = c(448,1462),
label = 'linoleic', values = ~linoleic),
list(range = c(-74,-20),
label = 'linolenic', values = ~(-linolenic)),
list(range = c(-102,-32),
label = 'arachidic', values = ~(-arachidic)),
list(range = c(-375,-152),
label = 'stearic', values = ~(-stearic))
)
)
olive_pcp
```
```{r}
#| eval: false
animate_xy(olive[,1:7], col=olive$area, rescale=TRUE)
```
The three areas are quite distinct. We could distinguish the growing area of the olive oils by examining the fatty acid composition.
:::
c. Re-do b. with Sicily. Explain what you learn about Sicily relative to the other areas.
::: unilur-solution
```{r}
#| label: pcp-all
# Now all four area
olive_pcp <- olive %>%
plot_ly(type = 'parcoords',
line = list(color = ~area,
colorscale = list(c(0,clrs[1]), c(0.33,clrs[2]),
c(0.67,clrs[3]), c(1,clrs[4]))),
dimensions = list(
list(range = c(35,280),
label = 'palmitoleic', values = ~palmitoleic),
list(range = c(-8113,-6300),
label = 'oleic', values = ~(-oleic)),
list(range = c(875,1753),
label = 'palmitic', values = ~palmitic),
list(range = c(448,1462),
label = 'linoleic', values = ~linoleic),
list(range = c(-74,-20),
label = 'linolenic', values = ~(-linolenic)),
list(range = c(-102,-32),
label = 'arachidic', values = ~(-arachidic)),
list(range = c(-375,-152),
label = 'stearic', values = ~(-stearic))
)
)
olive_pcp
```
```{r}
#| eval: false
animate_xy(olive[,1:7], col=olive$area, rescale=TRUE)
```
 Sicily overlaps with two of the other three areas. Most of the samples are not distinguishable from the other two.
:::
d. Use your AI helper or do some googling. What can you find out about Sicilian olive oils? Are they higher in value? Does Sicily even grow olives, or does it use olives from neighbouring areas?
::: unilur-solution
Not sure what the reason is! Maybe growing conditions in some fields are similar in the three areas. Probably the best explanation is that Sicily imports olives from neighbouring areas to make the oils.
:::
## Exercise 3: Baker field soils
The data measures essential elements in the soils for agricultural uses in the Baker field in Iowa. Some of these variables are skewed, which makes examining associations between them and other variables less useful. It can help to transform skewed variables to be more symmetric and then check for associations. This is what we will do here.
```{r}
#| label: corn
#| message: false
corn <- read_csv("https://eda.numbat.space/data/baker.csv")
```
a. Make density plots of the soil variables in the Baker field corn yield data. Choose an appropriate transformation to symmetrise the distribution.
::: unilur-solution
Many of the variables have a right-skewed distribution. For this thinking about a square root or log transformation would be appropriate. Ca has a severe right-skew, so a log-log transformation might be required. The code below shows the transformations made.
```{r}
corn_long <- corn %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
corn_trf <- corn %>%
mutate(B = log10(B),
Ca = log10(log10(Ca)),
Cu = sqrt(Cu),
K = log10(K),
Mg = sqrt(Mg),
Mn = sqrt(Mn),
Na = sqrt(Na),
P = log10(P),
Zn = sqrt(Zn))
corn_long <- corn_trf %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
```
The transformed data has mostly symmetric, unimodal distributions now. Making these transformations is useful when considering the relationship between variables. If each variable is well-spread then the association is measured using most of the points, but if you try to assess the association between skewed distributions, the judgement is based on just a handful of observations.
:::
b. Examine the pairwise associations using an interactive scatterplot matrix. Describe what you learn.
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 8
#| message: false
highlight_key(corn_trf) %>%
ggpairs(columns=4:13) %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Strong positive linear association: eg Ca-Cu, K-P
- Weak negative linear association: Fe-Ca
- Potential outliers: univariate Na; bivariate Ca-Cu
- Nonlinear association: Fe-Cu
I don't know what these mean, but the non-linear relationship is interesting.
When Fe is low,
- Cu is high, then Ca and other variables like Mg are high.
- Cu is low, then Ca and other variables like Mg are low
When Fe is high, the relationship between Ca and Cu (and Ca-Mg) is very strongly positive.
:::
c. Using a grand tour, how would you answer the following questions? Is there clustering? Is there linear dependence? Non-linear dependence? outliers. For any structure that you see determine which variables contribute to it, and make plots of these variables (or check the scatterplot matrix) to check whether the pattern is visible there too.
::: unilur-solution
```{r}
#| eval: false
animate_xy(corn_trf[,4:13], rescale = TRUE)
```
Sicily overlaps with two of the other three areas. Most of the samples are not distinguishable from the other two.
:::
d. Use your AI helper or do some googling. What can you find out about Sicilian olive oils? Are they higher in value? Does Sicily even grow olives, or does it use olives from neighbouring areas?
::: unilur-solution
Not sure what the reason is! Maybe growing conditions in some fields are similar in the three areas. Probably the best explanation is that Sicily imports olives from neighbouring areas to make the oils.
:::
## Exercise 3: Baker field soils
The data measures essential elements in the soils for agricultural uses in the Baker field in Iowa. Some of these variables are skewed, which makes examining associations between them and other variables less useful. It can help to transform skewed variables to be more symmetric and then check for associations. This is what we will do here.
```{r}
#| label: corn
#| message: false
corn <- read_csv("https://eda.numbat.space/data/baker.csv")
```
a. Make density plots of the soil variables in the Baker field corn yield data. Choose an appropriate transformation to symmetrise the distribution.
::: unilur-solution
Many of the variables have a right-skewed distribution. For this thinking about a square root or log transformation would be appropriate. Ca has a severe right-skew, so a log-log transformation might be required. The code below shows the transformations made.
```{r}
corn_long <- corn %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
corn_trf <- corn %>%
mutate(B = log10(B),
Ca = log10(log10(Ca)),
Cu = sqrt(Cu),
K = log10(K),
Mg = sqrt(Mg),
Mn = sqrt(Mn),
Na = sqrt(Na),
P = log10(P),
Zn = sqrt(Zn))
corn_long <- corn_trf %>%
select(B:Zn) %>%
pivot_longer(everything(),
names_to="var",
values_to="value")
ggplot(corn_long, aes(x=value)) +
geom_density() +
facet_wrap(~var, ncol=4, scales="free")
```
The transformed data has mostly symmetric, unimodal distributions now. Making these transformations is useful when considering the relationship between variables. If each variable is well-spread then the association is measured using most of the points, but if you try to assess the association between skewed distributions, the judgement is based on just a handful of observations.
:::
b. Examine the pairwise associations using an interactive scatterplot matrix. Describe what you learn.
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 8
#| message: false
highlight_key(corn_trf) %>%
ggpairs(columns=4:13) %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Strong positive linear association: eg Ca-Cu, K-P
- Weak negative linear association: Fe-Ca
- Potential outliers: univariate Na; bivariate Ca-Cu
- Nonlinear association: Fe-Cu
I don't know what these mean, but the non-linear relationship is interesting.
When Fe is low,
- Cu is high, then Ca and other variables like Mg are high.
- Cu is low, then Ca and other variables like Mg are low
When Fe is high, the relationship between Ca and Cu (and Ca-Mg) is very strongly positive.
:::
c. Using a grand tour, how would you answer the following questions? Is there clustering? Is there linear dependence? Non-linear dependence? outliers. For any structure that you see determine which variables contribute to it, and make plots of these variables (or check the scatterplot matrix) to check whether the pattern is visible there too.
::: unilur-solution
```{r}
#| eval: false
animate_xy(corn_trf[,4:13], rescale = TRUE)
```


 - There is no clustering.
- There is linear dependence, quite strong.
- There is a small amount of non-linear dependence.
- There are some outliers. See third snapshot above, to see non-linear dependence and outliers, when primarily Fe and Na are combined. This was not visible in the pairwise plot.
:::
## Exercise 4: Exam marks
There is a dataset `mathmarks` in the SMPracticals package, which has marks out of 100 for 88 students. It is interesting to note that all students had marks for all tests, which makes one wonder whether marks for students who missed a test were dropped. Mechanics and vectors were closed book exams, and the others were open book.
```{r math}
#| label: math
data(mathmarks, package="SMPracticals")
```
a. Make a side-by-side boxplot of the test scores. What do you learn about the test scores on the different subjects?
::: unilur-solution
```{r}
mathmarks %>%
pivot_longer(everything(), names_to="var", values_to="marks") %>%
mutate(var = factor(var, levels=unique(var))) %>%
ggplot(aes(x=var, y=marks)) +
geom_boxplot()
```
There is some difference in median and IQR across exams. Students tended to do better on vectors, algebra and analysis and worse on mechanics and statistics. There is no indication that the open book exams produced better scores than the closed book exams.
The distributions are fairly symmetric. The spread is similar except for algebra which are more concentrated. There is one quite high score on algebra, and two low scores. Mechanics and vectors has an unusually low score each.
:::
b. Make a scatterplot matrix, even better if it is interactive. Describe the relationships between the tests. Is there something different about the open book vs closed book scores?
::: unilur-solution
```{r}
#| message: false
#| fig-width: 8
#| fig-height: 8
highlight_key(mathmarks) %>%
ggpairs() %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Generally we can see positive linear association. Algebra and analysis are most related. Algebra is pretty closely related to all other test scores. Mechanics is only weakly related to statistics.
- There are a couple of outliers: low scores on algebra, and also two students who did badly on vectors but quite well on analysis.
- There looks to be a barrier at 80 for the statistics test, maybe this was the maximum possible score.
- Analysis and algebra, and also analysis and vectors has what I call a "comet" distribution: there is a tight concentration of high scores, and a big spread among lower scores. I see this a lot in statistics test scores.
:::
c. Make an interactive parallel coordinate plot. Are there some students who have done consistently well on all tests? Consistently badly on all tests? Badly on some but better on others?
::: unilur-solution
```{r}
marks_pcp <- mathmarks %>%
plot_ly(type = 'parcoords',
dimensions = list(
list(range = c(0,100),
label = 'mechanics', values = ~mechanics),
list(range = c(0,100),
label = 'vectors', values = ~vectors),
list(range = c(0,100),
label = 'algebra', values = ~algebra),
list(range = c(1,100),
label = 'analysis', values = ~analysis),
list(range = c(1,100),
label = 'statistics', values = ~statistics)
)
)
marks_pcp
```
- There is one student who did poorly on the closed book exams, but relatively better on the open book exams.
- There is one student who did really well on the closed book vectors exam, but badly on all other exams.
- There are a few students who have done really well on all exams.
- Generally, a student does relatively as well across all the tests. - There appears to be some slight bimodality or multimodality in mechanics, analysis and statistics which is also visible in the density plots in the splom.
:::
## Exercise 5: Knowledge and resources
The `vcdExtra` package contains a dataset `Dyke` about how 1729 survey respondents' knowledge of cancer depended on whether they listened to the radio, read newspapers, did solid reading, or attended lectures. This data is all categorical, so we need to make plots to show the relationships between five categorical variables.
```{r}
data(Dyke, package="vcdExtra")
```
a. Make separate bar charts for each of the explanatory variables, with bars filled by the response variable `Knowledge`. What do you learn?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
Dyke_tsb <- as_tibble(Dyke) %>%
mutate(Knowledge = factor(Knowledge, levels=c("Good", "Poor")),
Reading = factor(Reading, levels=c("Yes", "No")),
Radio = factor(Radio, levels=c("Yes", "No")),
Lectures = factor(Lectures, levels=c("Yes", "No")),
Newspaper = factor(Newspaper, levels=c("Yes", "No")))
p1 <- ggplot(Dyke_tsb, aes(x=Reading, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p2 <- ggplot(Dyke_tsb, aes(x=Radio, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
scale_fill_discrete_divergingx(palette="Zissou 1")
p3 <- ggplot(Dyke_tsb, aes(x=Lectures, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p4 <- ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p1 + p2 + p3 + p4 + plot_layout(ncol=4,
guides="collect") &
theme(legend.position = "bottom", legend.direction = "horizontal")
```
The focus here is on counts, and it is hard to read proportions. We learn that there are
- roughly equal numbers of Yes/No in Reading, and similarly in Newspaper.
- but much fewer people listen to the Radio or attend Lectures.
:::
b. Make a 100% bar chart of Newspaper, with Knowledge mapped to fill, and faceted by Reading. What do you learn about the relative proportions in the groups?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_bar(stat="identity",
position = position_fill(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1") +
facet_wrap(~Reading, labeller=labeller(Reading=label_both))
```
- When Reading is Yes, Knowledge is more likely to be good, than if Reading is No.
- When Newspaper is Yes, in both Reading Yes and No, Knowledge is more likely to be Good, then if Newspaper is No.
:::
c. Make a doubledecker plot of the data. What combination of factors leads to the highest level of knowledge about cancer? What combination leads to the lowest?
```{r}
#| echo: true
#| eval: false
#| label: knowledge-dd
# I had a difficult time getting the Good category being the first
# and to be coloured red, but this appears to work
Dyke_tbl <- Dyke_tsb %>%
mutate(Knowledge = factor(Knowledge, levels=c("Poor", "Good"))) %>%
uncount(n) %>%
select(Reading, Radio, Lectures, Newspaper, Knowledge) %>%
arrange(Knowledge, Reading, Radio, Lectures, Newspaper)
doubledecker(Knowledge~., Dyke_tbl,
gp = gpar(fill=c("grey90", "orangered")))
```
::: unilur-solution
```{r}
#| echo: false
#| eval: true
#| label: knowledge-dd
```
From the double-decker plot, it is much easier to read off which combinations of factors yields the higher knowledge.
The most knowledgeable people read, listen to the radio, attend lectures and read newspapers - as might be expected. There a very few people in this category, though. On each comparison the Yes group is more knowledgeable than the No group. The most populous group is the No to all combination. This is pretty shocking because it is the least knowledgeable about cancer. The second most common group are people who read newspapers, and read generally, and these are relatively knowledgeable about cancer.
:::
## Exercise 6: Parkinsons
This dataset is composed of a range of biomedical voice measurements from 31 people, 23 with Parkinson's disease (PD). Each column in the table is a particular voice measure, and each row corresponds one of 195 voice recording from these individuals ("name" column). The main aim of the data is to discriminate healthy people from those with PD, according to "status" column which is set to 0 for healthy and 1 for PD.
The data is available at [The UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Parkinsons) in ASCII CSV format. The rows of the CSV file contain an instance corresponding to one voice recording. There are around six recordings per patient, the name of the patient is identified in the first column. There are 24 variables in the file, including the persons name in column 1.
The data are originally analysed in:
Max A. Little, Patrick E. McSharry, Eric J. Hunter, Lorraine O. Ramig (2008), 'Suitability of dysphonia measurements for telemonitoring of Parkinson's disease', IEEE Transactions on Biomedical Engineering (to appear).
```{r}
#| eval: true
#| echo: true
library(cassowaryr)
# Load the data
data(pk)
```
a. How many pairwise plots would you need to look at, to look at all of them?
::: unilur-solution
There are 23 numeric variables in the data set, which would require `r 23*22/2` pairwise plots to be made.
:::
b. Compute several of the scagnostics (monotonic, outlying, clumpy2) for the first five variables of variables, except for `name`. (*Note*: We are using just five for computing speed, but the scagnostics could be calculated on all variables.)
```{r}
#| eval: false
#| echo: true
#| label: pk
# Compute the scagnostics on the relevant variables
s <- calc_scags_wide(pk[,2:5],
scags=c("outlying","monotonic",
"clumpy2"))
s
```
::: unilur-solution
```{r}
#| eval: true
#| echo: false
#| message: false
#| label: pk
```
:::
c. Sort the scagnostics, separately by the values on (i) monotonic (ii) outlying (iii) clumpy2, and plot the pair of variables with the highest values on each.
::: unilur-solution
```{r}
# Check the results for monotonic
s %>%
select(Var1, Var2, monotonic) %>%
arrange(desc(monotonic))
ggplot(data=pk,
aes(x=`MDVP:Fhi(Hz)`, y=`MDVP:Fo(Hz)`)) +
geom_point() + theme(aspect.ratio = 1)
```
The top pair of variables on monotonic has a strong positive association with the majority of points, and a few outliers. The top pair of variables on outlying, is also the top pair on clumpy2, and has outliers with some clumpiness in the mass of points with low values.
:::
d. Make an interactive scatterplot matrix. Browse over it to choose other interesting pairs of variables and make the plots.
::: unilur-solution
```{r}
#| message: false
# Create an interactive splom
s <- s %>%
mutate(vars = paste(Var1, Var2))
highlight_key(s) %>%
GGally::ggpairs(columns = 3:5, mapping = aes(label = vars)) %>%
ggplotly(tooltip = "all",
width=500,
height=500) %>%
highlight("plotly_selected")
```
:::
e. The scagnostics help us to find interesting associations between pairs of variables. However, the problem here is to detect differences between Parkinsons patients and normal patients. How would you go about that? Think about some ideas long the line of scagnostics but look for differences between the two groups.
::: unilur-solution
```{r}
# One way to examine difference between Parkinsons and healthy
pk_med <- pk %>%
select(-name) %>%
group_by(status) %>%
summarise_all(list(median, sd)) %>%
pivot_longer(
cols=`MDVP:Fo(Hz)_fn1`:`PPE_fn2`,
names_to="var",
values_to="value") %>%
separate(var, c("var","stat"), "_") %>%
mutate(stat = fct_recode(stat,
"m"="fn1",
"s"="fn2")) %>%
pivot_wider(names_from=stat,
values_from=value) %>%
group_by(var) %>%
summarise(
d = (m[status==0]-m[status==1])/sqrt(s[status==0]^2+s[status==1]^2))
pk_med %>% arrange(desc(d)) %>% head()
ggplot(pk, aes(x=factor(status), y=`MDVP:Fo(Hz)`)) +
geom_boxplot()
```
Generally we are looking for variables where the differences between the Parkinsons and normal patients are big. You need to measure big, relative to the variance of each group. Doing a two sample t-test for each variable is one approach. Here, I've computed the median for each group of patients and compared the difference in medians relative to the pooled standard deviation in each group.
:::
## `r emo::ji("wave")` Finishing up
Make sure you say thanks and good-bye to your tutor. This is a time to also report what you enjoyed and what you found difficult.
- There is no clustering.
- There is linear dependence, quite strong.
- There is a small amount of non-linear dependence.
- There are some outliers. See third snapshot above, to see non-linear dependence and outliers, when primarily Fe and Na are combined. This was not visible in the pairwise plot.
:::
## Exercise 4: Exam marks
There is a dataset `mathmarks` in the SMPracticals package, which has marks out of 100 for 88 students. It is interesting to note that all students had marks for all tests, which makes one wonder whether marks for students who missed a test were dropped. Mechanics and vectors were closed book exams, and the others were open book.
```{r math}
#| label: math
data(mathmarks, package="SMPracticals")
```
a. Make a side-by-side boxplot of the test scores. What do you learn about the test scores on the different subjects?
::: unilur-solution
```{r}
mathmarks %>%
pivot_longer(everything(), names_to="var", values_to="marks") %>%
mutate(var = factor(var, levels=unique(var))) %>%
ggplot(aes(x=var, y=marks)) +
geom_boxplot()
```
There is some difference in median and IQR across exams. Students tended to do better on vectors, algebra and analysis and worse on mechanics and statistics. There is no indication that the open book exams produced better scores than the closed book exams.
The distributions are fairly symmetric. The spread is similar except for algebra which are more concentrated. There is one quite high score on algebra, and two low scores. Mechanics and vectors has an unusually low score each.
:::
b. Make a scatterplot matrix, even better if it is interactive. Describe the relationships between the tests. Is there something different about the open book vs closed book scores?
::: unilur-solution
```{r}
#| message: false
#| fig-width: 8
#| fig-height: 8
highlight_key(mathmarks) %>%
ggpairs() %>%
ggplotly() %>%
highlight("plotly_selected")
```
- Generally we can see positive linear association. Algebra and analysis are most related. Algebra is pretty closely related to all other test scores. Mechanics is only weakly related to statistics.
- There are a couple of outliers: low scores on algebra, and also two students who did badly on vectors but quite well on analysis.
- There looks to be a barrier at 80 for the statistics test, maybe this was the maximum possible score.
- Analysis and algebra, and also analysis and vectors has what I call a "comet" distribution: there is a tight concentration of high scores, and a big spread among lower scores. I see this a lot in statistics test scores.
:::
c. Make an interactive parallel coordinate plot. Are there some students who have done consistently well on all tests? Consistently badly on all tests? Badly on some but better on others?
::: unilur-solution
```{r}
marks_pcp <- mathmarks %>%
plot_ly(type = 'parcoords',
dimensions = list(
list(range = c(0,100),
label = 'mechanics', values = ~mechanics),
list(range = c(0,100),
label = 'vectors', values = ~vectors),
list(range = c(0,100),
label = 'algebra', values = ~algebra),
list(range = c(1,100),
label = 'analysis', values = ~analysis),
list(range = c(1,100),
label = 'statistics', values = ~statistics)
)
)
marks_pcp
```
- There is one student who did poorly on the closed book exams, but relatively better on the open book exams.
- There is one student who did really well on the closed book vectors exam, but badly on all other exams.
- There are a few students who have done really well on all exams.
- Generally, a student does relatively as well across all the tests. - There appears to be some slight bimodality or multimodality in mechanics, analysis and statistics which is also visible in the density plots in the splom.
:::
## Exercise 5: Knowledge and resources
The `vcdExtra` package contains a dataset `Dyke` about how 1729 survey respondents' knowledge of cancer depended on whether they listened to the radio, read newspapers, did solid reading, or attended lectures. This data is all categorical, so we need to make plots to show the relationships between five categorical variables.
```{r}
data(Dyke, package="vcdExtra")
```
a. Make separate bar charts for each of the explanatory variables, with bars filled by the response variable `Knowledge`. What do you learn?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
Dyke_tsb <- as_tibble(Dyke) %>%
mutate(Knowledge = factor(Knowledge, levels=c("Good", "Poor")),
Reading = factor(Reading, levels=c("Yes", "No")),
Radio = factor(Radio, levels=c("Yes", "No")),
Lectures = factor(Lectures, levels=c("Yes", "No")),
Newspaper = factor(Newspaper, levels=c("Yes", "No")))
p1 <- ggplot(Dyke_tsb, aes(x=Reading, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p2 <- ggplot(Dyke_tsb, aes(x=Radio, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
scale_fill_discrete_divergingx(palette="Zissou 1")
p3 <- ggplot(Dyke_tsb, aes(x=Lectures, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p4 <- ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_col(position = position_stack(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1")
p1 + p2 + p3 + p4 + plot_layout(ncol=4,
guides="collect") &
theme(legend.position = "bottom", legend.direction = "horizontal")
```
The focus here is on counts, and it is hard to read proportions. We learn that there are
- roughly equal numbers of Yes/No in Reading, and similarly in Newspaper.
- but much fewer people listen to the Radio or attend Lectures.
:::
b. Make a 100% bar chart of Newspaper, with Knowledge mapped to fill, and faceted by Reading. What do you learn about the relative proportions in the groups?
::: unilur-solution
```{r}
#| fig-width: 8
#| fig-height: 4
ggplot(Dyke_tsb, aes(x=Newspaper, fill=Knowledge, y=n)) +
geom_bar(stat="identity",
position = position_fill(reverse = TRUE)) +
ylab("") +
scale_fill_discrete_divergingx(palette="Zissou 1") +
facet_wrap(~Reading, labeller=labeller(Reading=label_both))
```
- When Reading is Yes, Knowledge is more likely to be good, than if Reading is No.
- When Newspaper is Yes, in both Reading Yes and No, Knowledge is more likely to be Good, then if Newspaper is No.
:::
c. Make a doubledecker plot of the data. What combination of factors leads to the highest level of knowledge about cancer? What combination leads to the lowest?
```{r}
#| echo: true
#| eval: false
#| label: knowledge-dd
# I had a difficult time getting the Good category being the first
# and to be coloured red, but this appears to work
Dyke_tbl <- Dyke_tsb %>%
mutate(Knowledge = factor(Knowledge, levels=c("Poor", "Good"))) %>%
uncount(n) %>%
select(Reading, Radio, Lectures, Newspaper, Knowledge) %>%
arrange(Knowledge, Reading, Radio, Lectures, Newspaper)
doubledecker(Knowledge~., Dyke_tbl,
gp = gpar(fill=c("grey90", "orangered")))
```
::: unilur-solution
```{r}
#| echo: false
#| eval: true
#| label: knowledge-dd
```
From the double-decker plot, it is much easier to read off which combinations of factors yields the higher knowledge.
The most knowledgeable people read, listen to the radio, attend lectures and read newspapers - as might be expected. There a very few people in this category, though. On each comparison the Yes group is more knowledgeable than the No group. The most populous group is the No to all combination. This is pretty shocking because it is the least knowledgeable about cancer. The second most common group are people who read newspapers, and read generally, and these are relatively knowledgeable about cancer.
:::
## Exercise 6: Parkinsons
This dataset is composed of a range of biomedical voice measurements from 31 people, 23 with Parkinson's disease (PD). Each column in the table is a particular voice measure, and each row corresponds one of 195 voice recording from these individuals ("name" column). The main aim of the data is to discriminate healthy people from those with PD, according to "status" column which is set to 0 for healthy and 1 for PD.
The data is available at [The UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Parkinsons) in ASCII CSV format. The rows of the CSV file contain an instance corresponding to one voice recording. There are around six recordings per patient, the name of the patient is identified in the first column. There are 24 variables in the file, including the persons name in column 1.
The data are originally analysed in:
Max A. Little, Patrick E. McSharry, Eric J. Hunter, Lorraine O. Ramig (2008), 'Suitability of dysphonia measurements for telemonitoring of Parkinson's disease', IEEE Transactions on Biomedical Engineering (to appear).
```{r}
#| eval: true
#| echo: true
library(cassowaryr)
# Load the data
data(pk)
```
a. How many pairwise plots would you need to look at, to look at all of them?
::: unilur-solution
There are 23 numeric variables in the data set, which would require `r 23*22/2` pairwise plots to be made.
:::
b. Compute several of the scagnostics (monotonic, outlying, clumpy2) for the first five variables of variables, except for `name`. (*Note*: We are using just five for computing speed, but the scagnostics could be calculated on all variables.)
```{r}
#| eval: false
#| echo: true
#| label: pk
# Compute the scagnostics on the relevant variables
s <- calc_scags_wide(pk[,2:5],
scags=c("outlying","monotonic",
"clumpy2"))
s
```
::: unilur-solution
```{r}
#| eval: true
#| echo: false
#| message: false
#| label: pk
```
:::
c. Sort the scagnostics, separately by the values on (i) monotonic (ii) outlying (iii) clumpy2, and plot the pair of variables with the highest values on each.
::: unilur-solution
```{r}
# Check the results for monotonic
s %>%
select(Var1, Var2, monotonic) %>%
arrange(desc(monotonic))
ggplot(data=pk,
aes(x=`MDVP:Fhi(Hz)`, y=`MDVP:Fo(Hz)`)) +
geom_point() + theme(aspect.ratio = 1)
```
The top pair of variables on monotonic has a strong positive association with the majority of points, and a few outliers. The top pair of variables on outlying, is also the top pair on clumpy2, and has outliers with some clumpiness in the mass of points with low values.
:::
d. Make an interactive scatterplot matrix. Browse over it to choose other interesting pairs of variables and make the plots.
::: unilur-solution
```{r}
#| message: false
# Create an interactive splom
s <- s %>%
mutate(vars = paste(Var1, Var2))
highlight_key(s) %>%
GGally::ggpairs(columns = 3:5, mapping = aes(label = vars)) %>%
ggplotly(tooltip = "all",
width=500,
height=500) %>%
highlight("plotly_selected")
```
:::
e. The scagnostics help us to find interesting associations between pairs of variables. However, the problem here is to detect differences between Parkinsons patients and normal patients. How would you go about that? Think about some ideas long the line of scagnostics but look for differences between the two groups.
::: unilur-solution
```{r}
# One way to examine difference between Parkinsons and healthy
pk_med <- pk %>%
select(-name) %>%
group_by(status) %>%
summarise_all(list(median, sd)) %>%
pivot_longer(
cols=`MDVP:Fo(Hz)_fn1`:`PPE_fn2`,
names_to="var",
values_to="value") %>%
separate(var, c("var","stat"), "_") %>%
mutate(stat = fct_recode(stat,
"m"="fn1",
"s"="fn2")) %>%
pivot_wider(names_from=stat,
values_from=value) %>%
group_by(var) %>%
summarise(
d = (m[status==0]-m[status==1])/sqrt(s[status==0]^2+s[status==1]^2))
pk_med %>% arrange(desc(d)) %>% head()
ggplot(pk, aes(x=factor(status), y=`MDVP:Fo(Hz)`)) +
geom_boxplot()
```
Generally we are looking for variables where the differences between the Parkinsons and normal patients are big. You need to measure big, relative to the variance of each group. Doing a two sample t-test for each variable is one approach. Here, I've computed the median for each group of patients and compared the difference in medians relative to the pooled standard deviation in each group.
:::
## `r emo::ji("wave")` Finishing up
Make sure you say thanks and good-bye to your tutor. This is a time to also report what you enjoyed and what you found difficult.